题目内容
若向量
=（3x，-5，4）与向量
=（x，2x，-2）之间的夹角为钝角，求实数x的取值范围．
| a |
| b |
考点：空间向量的夹角与距离求解公式
专题：空间向量及应用
分析：由题意可得
•
＜0且
与
不共线，解不等式排除共线的情形即可．
| a |
| b |
| a |
| b |
解答：
解：∵向量
=（3x，-5，4）与向量
=（x，2x，-2）之间的夹角为钝角，
∴
•
＜0且
与
不共线，由
•
＜0可得3x2-10x-8＜0，
分解因式可得（x-4）（3x+2）＜0，解得-
＜x＜4，
当
与
共线时，
=
=
，可得该方程组无解，
∴实数x的取值范围为：-
＜x＜4
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
分解因式可得（x-4）（3x+2）＜0，解得-
| 2 |
| 3 |
当
| a |
| b |
| 3x |
| x |
| -5 |
| 2x |
| 4 |
| -2 |
∴实数x的取值范围为：-
| 2 |
| 3 |
点评：本题考查空间向量的夹角，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
设a=90.8，b=270.45，c=（
）-1.5，则a，b，c大小关系为（ ）
| 1 |
| 3 |
| A、a＞b＞c |
| B、a＜b＜c |
| C、a＞c＞b |
| D、b＞c＞a |
如图，在边长为1的正方形OABC中任取一点P，分数以O、B为圆心，半径为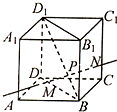
正方体ABCD-A1B1C1D1，P在BD1上，过P作垂直于BD1的平面α，记这样得到的截面多边形（含三角形）周长为y，为什么当α在平面AB1C，面A1DC1之间运动时，y不变？
如图，四棱柱的底面是菱形，各侧面都是长方形，两个对角面也是长方形，面积分别为Q1，Q．求四棱柱的侧面积．在半径为5的圆中，圆心角为周长的
的角所对圆弧的长是（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在约束条件
下，若目标函数z=-2x+y的最大值不超过4，则实数m的取值范围（ ）
|
A、（-
| ||||
B、[0，
| ||||
C、[-
| ||||
D、[-
|