题目内容
设f(x)=x(
+
),
(1)求函数f(x)的定义域;
(2)证明:对于任意非零实数都有f(x)>0.
| 1 |
| 2x-1 |
| 1 |
| 2 |
(1)求函数f(x)的定义域;
(2)证明:对于任意非零实数都有f(x)>0.
考点:函数恒成立问题,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)函数有意义则分母2x-1≠0得其定义域,(2)当x>0时明显成立,当x<0时,先证f(-x)=f(x),函数为奇函数,然后由-x>0转化求解.
解答:
解:(1)由2x-1≠0得x≠0,故函数f(x)的定义域是(-∞,0)∪(0,+∞)
(2)证明:当x>0时,因为2x>1,显然f(x)>0
因为f(-x)=-x(
+
)=-x(
+
)
=x(
-
)=x(
-
)=x(
+
)
=f(x)
所以,当x<0时,-x>0,故f(x)=f(-x)>0
综上,f(x)>0,命题得证.
(2)证明:当x>0时,因为2x>1,显然f(x)>0
因为f(-x)=-x(
| 1 |
| 2-x-1 |
| 1 |
| 2 |
| 2x |
| 1-2x |
| 1 |
| 2 |
=x(
| 2x |
| 2x-1 |
| 1 |
| 2 |
| 2x-1+1 |
| 2x-1 |
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
=f(x)
所以,当x<0时,-x>0,故f(x)=f(-x)>0
综上,f(x)>0,命题得证.
点评:本题考察函数的定义域及其求法以及利用函数性质求证不等式,难点在证明中利用分类讨论和函数的奇偶性求证.

练习册系列答案
相关题目
设a=90.8,b=270.45,c=(
)-1.5,则a,b,c大小关系为( )
| 1 |
| 3 |
| A、a>b>c |
| B、a<b<c |
| C、a>c>b |
| D、b>c>a |
已知A={x|-2<x<4},B={y|y=|x+1|,x∈A},则A∩B=( )
| A、∅ |
| B、{x|1<x<4} |
| C、{x|-2<x<5} |
| D、{x|0≤x<4} |
在约束条件
下,若目标函数z=-2x+y的最大值不超过4,则实数m的取值范围( )
|
A、(-
| ||||
B、[0,
| ||||
C、[-
| ||||
D、[-
|
 如图,在边长为1的正方形OABC中任取一点P,分数以O、B为圆心,半径为
如图,在边长为1的正方形OABC中任取一点P,分数以O、B为圆心,半径为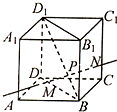 正方体ABCD-A1B1C1D1,P在BD1上,过P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)周长为y,为什么当α在平面AB1C,面A1DC1之间运动时,y不变?
正方体ABCD-A1B1C1D1,P在BD1上,过P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)周长为y,为什么当α在平面AB1C,面A1DC1之间运动时,y不变?