题目内容
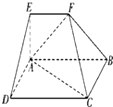 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=1,平面ABEF⊥平面ABCD,则点D到平面BCF的距离为考点:点、线、面间的距离计算
专题:计算题,作图题,空间位置关系与距离
分析:由题意作出图象,则可将点D到平面BCF的距离可化为点A到平面BCF的距离,再转化为平面ABEF内点A到直线BF的距离,从而利用面积相等求解.
解答:
 解:如右图,∵四边形ABCD是矩形,
解:如右图,∵四边形ABCD是矩形,
∴AD∥BC,
∴点D到平面BCF的距离可化为点A到平面BCF的距离,
又∵平面ABEF⊥平面ABCD,
∴平面BCF⊥平面ABEF,
∴点A到平面BCF的距离可化为平面ABEF内点A到直线BF的距离,
则在平面ABEF内,
BF=
,
则
×
×h=
×4×1,
则h=
.
故答案为:
.
 解:如右图,∵四边形ABCD是矩形,
解:如右图,∵四边形ABCD是矩形,∴AD∥BC,
∴点D到平面BCF的距离可化为点A到平面BCF的距离,
又∵平面ABEF⊥平面ABCD,
∴平面BCF⊥平面ABEF,
∴点A到平面BCF的距离可化为平面ABEF内点A到直线BF的距离,
则在平面ABEF内,
BF=
| 10 |
则
| 1 |
| 2 |
| 10 |
| 1 |
| 2 |
则h=
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题考查了学生的作图能力与转化能力,属于中档题.

练习册系列答案
相关题目
在约束条件
下,若目标函数z=-2x+y的最大值不超过4,则实数m的取值范围( )
|
A、(-
| ||||
B、[0,
| ||||
C、[-
| ||||
D、[-
|
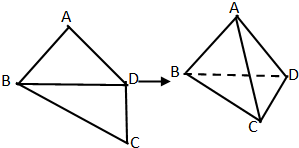 如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=
如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AD⊥平面ABC |
已知函数f(x)=x3+x2+x+1,则f(x)在(0,1)处的切线方程为( )
| A、x-y-1=0 |
| B、x+y+1=0 |
| C、x-y+1=0 |
| D、x+y-1=0 |
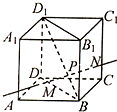 正方体ABCD-A1B1C1D1,P在BD1上,过P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)周长为y,为什么当α在平面AB1C,面A1DC1之间运动时,y不变?
正方体ABCD-A1B1C1D1,P在BD1上,过P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)周长为y,为什么当α在平面AB1C,面A1DC1之间运动时,y不变?