题目内容
已知各项均为正数的数列{an}前n项和为Sn,首项为2,且2,an,Sn成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2an,cn=
,求数列{cn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2an,cn=
| bn |
| an |
考点:数列的求和,等差数列的性质
专题:函数的性质及应用
分析:(Ⅰ)由已知条件推导出
=2,从而数列{an}是以2为首项,2为公比的等比数列.由此能求出数列{an}的通项公式.
(Ⅱ)由(Ⅰ)知an=2n,从而bn=n,cn=
,由此利用错位相减法能求出数列{cn}的前n项和Tn.
| an |
| an-1 |
(Ⅱ)由(Ⅰ)知an=2n,从而bn=n,cn=
| n |
| 2n |
解答:
解:(Ⅰ)由题意知2an=Sn+2,an>0,a1=2,(1分)
当n≥2时,Sn=2an-2,Sn-1=2an-1-2,
两式相减得an=2an-2an-1
整理得:
=2,(4分)
∴数列{an}是以2为首项,2为公比的等比数列.
∴an=a1•2n-1=2×2n-1=2n.(6分)
(Ⅱ)由(Ⅰ)知an=2n,∴bn=n,cn=
,(7分)
Tn=
+
+
+…+
,…①
Tn=
+
+
+…+
,…②
①-②得
Tn=
+
+
+
+…+
-
,(10分)
∴
Tn=1-
-
,(11分)
∴Tn=2-
.(12分)
当n≥2时,Sn=2an-2,Sn-1=2an-1-2,
两式相减得an=2an-2an-1
整理得:
| an |
| an-1 |
∴数列{an}是以2为首项,2为公比的等比数列.
∴an=a1•2n-1=2×2n-1=2n.(6分)
(Ⅱ)由(Ⅰ)知an=2n,∴bn=n,cn=
| n |
| 2n |
Tn=
| 1 |
| 2 |
| 2 |
| 4 |
| 3 |
| 8 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 8 |
| 3 |
| 16 |
| n |
| 2n+1 |
①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴
| 1 |
| 2 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-
| 2+n |
| 2n |
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在约束条件
下,若目标函数z=-2x+y的最大值不超过4,则实数m的取值范围( )
|
A、(-
| ||||
B、[0,
| ||||
C、[-
| ||||
D、[-
|
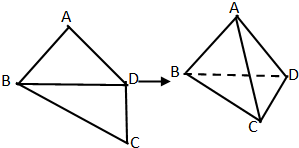 如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=
如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AD⊥平面ABC |
已知函数f(x)=x3+x2+x+1,则f(x)在(0,1)处的切线方程为( )
| A、x-y-1=0 |
| B、x+y+1=0 |
| C、x-y+1=0 |
| D、x+y-1=0 |