题目内容
已知数列{an}的首项a1=1,且满足an+1=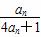 (n∈N*).
(n∈N*).
(1)设bn=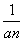 ,求证:数列{bn}是等差数列,并求数列{an}的通项公式;
,求证:数列{bn}是等差数列,并求数列{an}的通项公式;
(2)设cn=bn·2n,求数列{cn}的前n项和Sn.
(1)b1= =1,
=1, ∴bn+1-bn=4.
∴bn+1-bn=4.
数列{bn}是以1为首项,4为公差的等差数列.
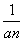 =bn=1+4(n-1)=4n-3,
=bn=1+4(n-1)=4n-3,
∴数列{an}的通项公式为an= (n∈N*).
(n∈N*).
(2)Sn=21+5×22+9×23+…+(4n-3)·2n,①
2Sn=22+5×23+9×24+…+(4n-3)·2n+1,②
②-①并化简得Sn=(4n-7)·2n+1+14.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
将正偶数按下表排成5列:
|
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第1行 |
| 2 | 4 | 6 | 8 |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 |
| 18 | 20 | 22 | 24 |
| …… |
| …… | 28 | 26 |
那么2014应该在第________行第________列.
 的值为________.
的值为________.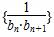 的前n项和Tn.
的前n项和Tn.