题目内容
{an}的前n项和为Sn,若(a2-1)3+2012(a2-1)=1,(a2011-1)3+2012·(a2011-1)=-1,则下列四个命题中真命题的序号为________.
①S2011=2011;②S2012=2012;③a2011<a2;④S2011<S2.
②③
[解析] 设f(x)=x3+2012x,则f(x)为奇函数,f ′(x)=3x2+2012>0,∴f(x)单调递增.由f(1)=2013>1知f(1)>f(a2-1),∴1>a2-1,∴a2<2.
又f(a2-1)=-f(a2011-1)=f(1-a2011),∴a2-1=1-a2011,∴a2+a2011=2,∴S2012=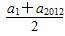 ×2012=2012,故②正确;
×2012=2012,故②正确;
又f(a2-1)>f(a2011-1),∴a2-1>a2011-1,
∴a2011<a2,∴③正确;
S2011=S2012-a2012=2012-(a2011+d)=2012-(2-a2+d)=2010+a1>a1+a2=S2,∴④错误;
假设S2011=2011,则2010+a1=2011,∴a1=1,
∵S2011=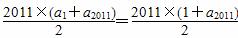 =2011,∴a2011=1,这与{an}是等差数列矛盾,∴①错.
=2011,∴a2011=1,这与{an}是等差数列矛盾,∴①错.
综上,正确的为②③.

练习册系列答案
相关题目
 (O为坐标原点)等于( )
(O为坐标原点)等于( ) =
= ,那么
,那么 等于( )
等于( ) B.
B. C.
C. D.
D.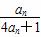 (n∈N*).
(n∈N*).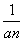 ,求证:数列{bn}是等差数列,并求数列{an}的通项公式;
,求证:数列{bn}是等差数列,并求数列{an}的通项公式;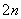 }的前n项的和为( )
}的前n项的和为( )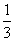 (4n-1)
(4n-1)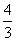 (4n-1) D.(2n-1)2
(4n-1) D.(2n-1)2
 与3的大小,并证明你的结论.
与3的大小,并证明你的结论.