题目内容
已知数列{an}的前n项和为Sn，a1＝1，且3an＋1＋2Sn＝3(n为正整数)．
(1)求出数列{an}的通项公式；
(2)若对任意正整数n，k≤Sn恒成立，求实数k的最大值．
(1)∵3an＋1＋2Sn＝3，①
∴当n≥2时，3an＋2Sn－1＝3，②
由①－②得，3an＋1－3an＋2an＝0.
∴
＝
(n≥2)．
又∵a1＝1,3a2＋2a1＝3，解得a2＝.
∴数列{an}是首项为1，公比q＝的等比数列．
∴an＝a1qn－1＝
n－1(n为正整数)．
(2)由(1)知，∴Sn＝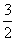
，
由题意可知，对于任意的正整数n，恒有
k≤，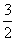
∵数列
单调递增，当n＝1时，数列取最小项为
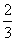，∴必有k≤1，即实数k的最大值为1.
练习册系列答案
相关题目
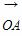＝(3，－4)，
＝(6，－3)，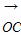
＝(5－m，－3－m)．
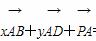＝0(x，y∈R)，则当点P在以A为圆心，
|
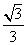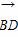|为半径的圆上时，实数x，y应满足关系式为( )
＝
，那么
等于( )
B.
C.
D.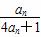
(n∈N*)．
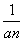，求证：数列{bn}是等差数列，并求数列{an}的通项公式；