题目内容
已知数列{an}中,a1=2,其前n项和Sn满足Sn+1-Sn=2n+1(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)令bn=2log2an+1,求数列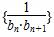 的前n项和Tn.
的前n项和Tn.
(1)由Sn+1-Sn=2n+1得an+1=2n+1,即an=2n(n≥2).
又a1=2,所以an=2n(n∈N*).
从而Sn=2+22+…+2n= =2n+1-2.
=2n+1-2.
(2)因为bn=2log2an+1=2log22n+1=2n+1,


练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
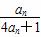 (n∈N*).
(n∈N*).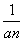 ,求证:数列{bn}是等差数列,并求数列{an}的通项公式;
,求证:数列{bn}是等差数列,并求数列{an}的通项公式;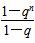 .判断{an}是否为等比数列,并证明你的结论.
.判断{an}是否为等比数列,并证明你的结论.
 =ad-bc.若不等式
=ad-bc.若不等式 ≥1对任意实数x恒成立,则实数a的最大值为( )
≥1对任意实数x恒成立,则实数a的最大值为( )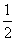 B.-
B.-
 D.
D.