若一个三角形的三个内角成等差数列.且已知一个角为30°.则另外两个角的度数分别为．题目和参考答案——青夏教育精英家教网—

题目内容

若一个三角形的三个内角成等差数列，且已知一个角为30°，则另外两个角的度数分别为

．

考点：等比数列的通项公式

专题：等差数列与等比数列

分析：设三个角的度数为α-d，α，α+d，由3α=180°，即α=60°，再由一个角为30°，求出另一个角为90°．

解答： 解：∵一个三角形的三个内角成等差数列，
∴设三个角的度数为α-d，α，α+d，
∴3α=180°，即α=60°，
又∵一个角为30°，
∴另一个角为90°．
∴另外两个角的度数分别为30°，90°．
故答案为：30°，90°．

点评：本题考查角的度数的求法，是基础题，解题时要认真审题，注意等等差数列的合理运用．

练习册系列答案

已知数列{a_n}中，a₁=1，a₂=4，满足a_n+2=

an+1-

an，则数列{a_n}的通项公式a_n=

．

已知曲线ax²+by²=12的两条动弦MA，MB所在直线的斜率分别为k₁，k₂．
（1）已知a=b=3且A（-2，0），B（2，0），试证明：k₁k₂为定值．
（2）已知a=3，b=4．
（i）若A（-2，0），B（2，0），试判断k₁k₂是否为定值？若是，求出定值；若不是，请说明理由．
（ii）若定点M（1，-

）且k₁k₂=

，试判断直线AB是否过一定点？若是，求出定点坐标；若不是，请说明理由．

在二项式(2

4	x

)n的展开式中，前三项的系数成等差数列，则该二项式展开式中x^-2项的系数为（　　）

x²-（2a+1）x+（4a-2）lnx（a∈R）．
（Ⅰ）若函数f（x）在x=3处取得极值，求曲线f（x）在点（1，f（1））处的切线方程；
（Ⅱ）当a≤

时，讨论f（x）的单调区间．

已知某几何体的三视图如图所示（单位cm），则此几何体的体积为（　　）

cm³

cm³

下列命题正确的是（　　）
①任何一个函数的定义域皆非空．
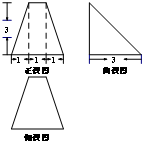
②直线x=a与函数f（x）图象有且仅有一个公共点．
③

n	5n

表示5的n次方根．
④若函数f（x）没有最大值，则f（x）一定趋近于+∞．
⑤若函数f（x）在[-1，0]单调递增且在[0，1]单调递增，则函数f（x）在[-1，1]一定单调递增．

A、①⑤	B、①③⑤
C、①②③④	D、①②④⑤

设等差数列的前n项和为S_n，已知前6项的和为36，S_n=324，最后6项的和为180（n＞6），求数列的项数n及a₉+a₁₀．

试题分类