题目内容
已知a,b,c∈R,a2+b2+c2=1.
(Ⅰ)求证:|a+b+c|≤
;
(Ⅱ)若不等式|x-1|+|x+1|≥(a+b+c)2对一切实数a,b,c恒成立,求实数x的取值范围.
(Ⅰ)求证:|a+b+c|≤
| 3 |
(Ⅱ)若不等式|x-1|+|x+1|≥(a+b+c)2对一切实数a,b,c恒成立,求实数x的取值范围.
考点:绝对值不等式的解法,不等式的证明
专题:计算题,证明题,不等式的解法及应用
分析:(Ⅰ)由柯西不等式得,(a+b+c)2≤(12+12+12)(a2+b2+c2),即可得证;
(Ⅱ)不等式|x-1|+|x+1|≥(a+b+c)2对一切实数a,b,c恒成立,则由(Ⅰ)可知,|x-1|+|x+1|≥3,运用绝对值的定义,即可解出不等式.
(Ⅱ)不等式|x-1|+|x+1|≥(a+b+c)2对一切实数a,b,c恒成立,则由(Ⅰ)可知,|x-1|+|x+1|≥3,运用绝对值的定义,即可解出不等式.
解答:
(Ⅰ)证明:由柯西不等式得,(a+b+c)2≤(12+12+12)(a2+b2+c2),
即有(a+b+c)2≤3,即有|a+b+c|≤
;
(Ⅱ)解:不等式|x-1|+|x+1|≥(a+b+c)2对一切实数a,b,c恒成立,
则由(Ⅰ)可知,|x-1|+|x+1|≥3,
由x≥1得,2x≥3,解得,x≥
;
由x≤-1,-2x≥3解得,x≤-
,
由-1<x<1得,2≥3,不成立.
综上,可得x≥
或x≤-
.
则实数x的取值范围是(-∞,-
]∪[
,+∞).
即有(a+b+c)2≤3,即有|a+b+c|≤
| 3 |
(Ⅱ)解:不等式|x-1|+|x+1|≥(a+b+c)2对一切实数a,b,c恒成立,
则由(Ⅰ)可知,|x-1|+|x+1|≥3,
由x≥1得,2x≥3,解得,x≥
| 3 |
| 2 |
由x≤-1,-2x≥3解得,x≤-
| 3 |
| 2 |
由-1<x<1得,2≥3,不成立.
综上,可得x≥
| 3 |
| 2 |
| 3 |
| 2 |
则实数x的取值范围是(-∞,-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查柯西不等式的运用,考查不等式恒成立问题,考查绝对值不等式的解法,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知x∈R,则
的最大值是( )
| |12cosx-5sinx+39| |
| 13 |
| A、2 | B、4 | C、13 | D、39 |
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6)上是单调函数,且f(-2)<f(1)则下列不等式成立的是( )
| A、f(-1)<f(1)<f(3) |
| B、f(2)<f(3)<f(-4) |
| C、f(-2)<f(0)<f(1) |
| D、f(5)<f(-3)<f(-1) |
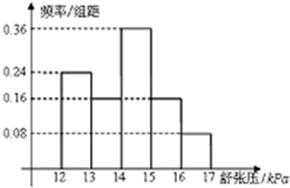 为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为
为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为