题目内容
已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x-2y-2=0.
(1)求f(x)的解析式;
(2)当x>1时,f(x)+
<0恒成立,求实数k的取值范围;
(3)设n是正整数,用n!表示前n个正整数的积,即n!=1•2•3…n.求证:n!<e
.
(1)求f(x)的解析式;
(2)当x>1时,f(x)+
| k |
| x |
(3)设n是正整数,用n!表示前n个正整数的积,即n!=1•2•3…n.求证:n!<e
| n(n+1) |
| 4 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)先求出函数f(x)的导函数,根据在x=1处的导数等于切线的斜率建立等量关系,以及切点在曲线上建立等式关系,解之即可.
(2)由题意可得k<
-xlnx.令g(x)=
-xlnx,则利用导数判断函数的单调性,求出函数g(x)的最小值即可;
(3)由(2)知,当x>1时,f(x)<0(k=0),又 x=1时f(x)<0也成立,所以当x≥1时,lnx<
,于是ln1<
,ln2<
,ln3<
,…,lnn<
,
上述各式相加即可得出结论.
(2)由题意可得k<
| x2 |
| 2 |
| x2 |
| 2 |
(3)由(2)知,当x>1时,f(x)<0(k=0),又 x=1时f(x)<0也成立,所以当x≥1时,lnx<
| x |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| n |
| 2 |
上述各式相加即可得出结论.
解答:
(1)解:∵f(x)=alnx+bx,∴f′(x)=
+b.
∵直线x-2y-2=0的斜率为
,且曲线y=f(x)过点(1,-
),
∴
,即
,解得a=1,b=-
.
所以 f(x)=lnx-
.
(2)解:由(1)得当x>1时,f(x)+
<0恒成立即 lnx-
+
<0,
等价于k<
-xlnx.
令g(x)=
-xlnx,则g′(x)=x-(lnx+1)=x-1-lnx.
令h(x)=x-1-lnx,则h′(x)=1-
=
.
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,故h(x)>h(1)=0.
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=
.
因此,当x>1时,k<
-xlnx.恒成立,则k≤
.
∴k的取值范围是(-∞,
].
(3)证明:由(2)知,当x>1时,f(x)<0(k=0),
又 x=1时f(x)<0也成立,
所以当x≥1时,lnx<
,于是
ln1<
,ln2<
,ln3<
,…,lnn<
,
上述各式相加得,ln(1×2×3×…×n)<
,
即lnn!<
,∴n!<e
.
| a |
| x |
∵直线x-2y-2=0的斜率为
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
|
| 1 |
| 2 |
所以 f(x)=lnx-
| x |
| 2 |
(2)解:由(1)得当x>1时,f(x)+
| k |
| x |
| x |
| 2 |
| k |
| x |
等价于k<
| x2 |
| 2 |
令g(x)=
| x2 |
| 2 |
令h(x)=x-1-lnx,则h′(x)=1-
| 1 |
| x |
| x-1 |
| x |
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,故h(x)>h(1)=0.
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=
| 1 |
| 2 |
因此,当x>1时,k<
| x2 |
| 2 |
| 1 |
| 2 |
∴k的取值范围是(-∞,
| 1 |
| 2 |
(3)证明:由(2)知,当x>1时,f(x)<0(k=0),
又 x=1时f(x)<0也成立,
所以当x≥1时,lnx<
| x |
| 2 |
ln1<
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| n |
| 2 |
上述各式相加得,ln(1×2×3×…×n)<
| 1+2+3+…+n |
| 2 |
即lnn!<
| n(n+1) |
| 4 |
| n(n+1) |
| 4 |
点评:本题主要考查导数的几何意义及利用导数研究函数的单调性、最值等知识,考查学生分析问题、解决问题的能力及运算求解能力,属于难题.

练习册系列答案
相关题目
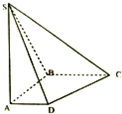 在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=