题目内容
已知向量|
|=|
|=2，且
•
=2，则|
+
|= ．
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：不妨取
=（2，0），
=（x，y），由于向量|
|=|
|=2，且
•
=2，可得
=2，2x=2，解出即可．
| a |
| b |
| a |
| b |
| a |
| b |
| x2+y2 |
解答：
解：不妨取
=（2，0），
=（x，y），
∵向量|
|=|
|=2，且
•
=2，
∴
=2，2x=2，
解得x=1，y=±
．
则|
+
|=|(3，±
)|=
=2
．
故答案为：2
．
| a |
| b |
∵向量|
| a |
| b |
| a |
| b |
∴
| x2+y2 |
解得x=1，y=±
| 3 |
则|
| a |
| b |
| 3 |
| 9+3 |
| 3 |
故答案为：2
| 3 |
点评：本题考查了向量的数量积运算、模的计算公式，属于基础题．
练习册系列答案
相关题目
已知向量
=（1，y，-2），
=（-2，2，z），若
∥
，则y+z=（ ）
| a |
| b |
| a |
| b |
| A、5 | B、3 | C、-3 | D、-5 |
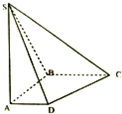在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=1，AD=