题目内容
下列命题中是错误命题的个数有( )
①A、B为两个事件,则P(A∪B)=P(A)+P(B);
②若事件A、B满足P(A)+P(B)=1,则A,B是对立事件
③A、B为两个事件,p(A|B)=P(B|A)
④若A、B为相互独立事件,则p(
B)=P(
)P(B).
①A、B为两个事件,则P(A∪B)=P(A)+P(B);
②若事件A、B满足P(A)+P(B)=1,则A,B是对立事件
③A、B为两个事件,p(A|B)=P(B|A)
④若A、B为相互独立事件,则p(
. |
| A |
. |
| A |
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:概率与统计
分析:①互斥事件概率加法公式,使用前提是事件互斥,②对立事件概率之和为1,但概率之和为1不一定对立,③条件概率的计算公式,书写错误,④由A、B为相互独立事件,
和B也是独立事件,利用独立事件概率公式计算.
. |
| A |
解答:
解:①只有A、B为两个互斥事件时,才有P(A∪B)=P(A)+P(B),否则,此式不成立,①错误,
②因为若事件A、B满足P(A)+P(B)=1,则A,B不一定是对立事件.如单位圆的一条直径把圆的面积分成相等的两部分,即区域M和区域N(不含边界),向这两个区域内投一枚绣花针,若针尖落在区域M内记为事件A,若针尖落在区域N内记为事件B,显然满足P(A)+P(B)=1,但A,B不是对立事件,因为针尖还有可能落在直径上,②错误,
③由条件概率的计算公式可得p(A|B)=
,③错误,
④由A、B为相互独立事件,可得
和B也是独立事件,故由独立事件的概率公式可得p(
B)=P(
)P(B).④正确,
综上,错误命题的个数是3个,
故选D.
②因为若事件A、B满足P(A)+P(B)=1,则A,B不一定是对立事件.如单位圆的一条直径把圆的面积分成相等的两部分,即区域M和区域N(不含边界),向这两个区域内投一枚绣花针,若针尖落在区域M内记为事件A,若针尖落在区域N内记为事件B,显然满足P(A)+P(B)=1,但A,B不是对立事件,因为针尖还有可能落在直径上,②错误,
③由条件概率的计算公式可得p(A|B)=
| P(AB) |
| P(B) |
④由A、B为相互独立事件,可得
. |
| A |
. |
| A |
. |
| A |
综上,错误命题的个数是3个,
故选D.
点评:本题考察随机事件及其概率中互斥事件,对立事件及相互独立事件概率的关系,要熟记概念,不可混淆,熟练运用公式,但容易在公式的使用条件上出错.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
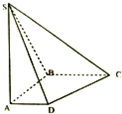 在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=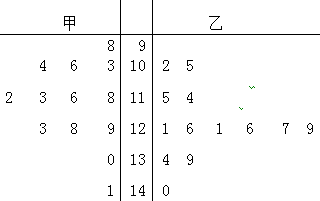
 一次学科测试成绩的频率分布直方图都受到不同程度的污损,可见部分如图.已知50~60分的有两个数,60~70分的有7个数,70~80分的有10个数,
一次学科测试成绩的频率分布直方图都受到不同程度的污损,可见部分如图.已知50~60分的有两个数,60~70分的有7个数,70~80分的有10个数,