题目内容
已知x∈R，则
的最大值是（ ）
| |12cosx-5sinx+39| |
| 13 |
| A、2 | B、4 | C、13 | D、39 |
考点：三角函数的最值
专题：三角函数的图像与性质
分析：直接利用两角和的正弦函数化简表达式，通过三角函数的最值求解即可．
解答：
解：x∈R，则
=
，其中tanθ=
，
≤
=4．
的最大值是：4．
故选：B．
| |12cosx-5sinx+39| |
| 13 |
| |13cos(x+θ)+39| |
| 13 |
| 5 |
| 12 |
| |13cos(x+θ)+39| |
| 13 |
| 13+39 |
| 13 |
| |12cosx-5sinx+39| |
| 13 |
故选：B．
点评：本题考查三角函数的化简求值，函数的最值的求法，两角和与差的三角函数的应用，是中档题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
已知向量
=（1，y，-2），
=（-2，2，z），若
∥
，则y+z=（ ）
| a |
| b |
| a |
| b |
| A、5 | B、3 | C、-3 | D、-5 |
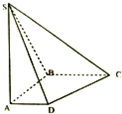在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=1，AD=
一次学科测试成绩的频率分布直方图都受到不同程度的污损，可见部分如图．已知50～60分的有两个数，60～70分的有7个数，70～80分的有10个数，