题目内容
15.把红桃、黑桃、方块、梅花四张纸牌随机发给甲、乙、丙、丁四个人,每人分得一张,事件“甲分得梅花”与事件“乙分得梅花”是( )| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上答案均不对 |
分析 利用互斥事件、对立事件的定义和性质直接求解.
解答 解:把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁四个人,每人分得1张,
事件“甲分得红牌”与事件“乙分得红牌”,由互斥事件和对立事件的概念可判断两者不可能同时发生,故它们是互斥事件,又事件“乙取得红牌”与事件“丙取得红牌”也是可能发生的,事件“甲分得红牌”与事件“乙分得红牌”不是对立事件,故两事件之间的关系是互斥而不对立,
故选C.
点评 本题考查互斥事件、对立事件的判断,是基础题,解题时要认真审题,注意互斥事件、对立事件的定义和性质的合理运用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
3.若函数f(x)=xex-m在R上存在两个不同的零点,则m的取值范围是( )
| A. | m>e | B. | m>-$\frac{1}{e}$ | C. | -$\frac{1}{e}$<m<0 | D. | -e<m<0 |
10.在等比数列{an}中,设a2=3,a5=81,bn=log3an,则数列{bn}的前n项和Sn为( )
| A. | $\frac{{{n^2}-n}}{2}$ | B. | $\frac{n^2}{2}$ | C. | $\frac{{{n^2}+n}}{2}$ | D. | $\frac{{{n^2}+2n}}{2}$ |
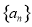 的前
的前 项和为
项和为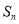 ,且
,且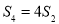 ,
,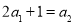 .
.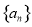 的通项公式;
的通项公式;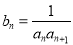 ,求
,求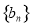 的前
的前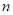 项和
项和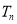 .
.