题目内容
19.观察下列等式: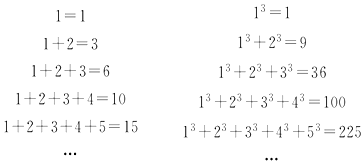
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |
分析 根据所给出的几个等式,可以看出,等式左边各项幂的底数的和等于右边的幂的底数,故可推测结论.
解答 解:根据所给等式13=12
13+23=32=(1+2)2
13+23+33=62=(1+2+3)2
13+23+33+43=102=(1+2+3+4)2…
可以看出,等式左边各项幂的底数的和等于右边的幂的底数,
推测:13+23+33+…+n3=(1+2+…+n)2=$\frac{1}{4}{n}^{2}(n+1)^{2}$
故选C.
点评 本题考查合情推理,解题的关键是根据所给等式,看出等式左边各项幂的底数的和等于右边的幂的底数.

练习册系列答案
相关题目
7.已知函数$f(x)=lg\frac{1+ax}{1-2x}$是定义在(-b,b)上的奇函数,(a,b∈R且a≠-2),则ab的取值范围是( )
| A. | $({1,\sqrt{2}}]$ | B. | $({0,\sqrt{2}}]$ | C. | $({1,\sqrt{2}})$ | D. | $({0,\sqrt{2}})$ |
4.在平行四边形ABCD中,对角线AC和BD的交点为M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则下列向量中与-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$相等的向量是( )
| A. | $\overrightarrow{MA}$ | B. | $\overrightarrow{MB}$ | C. | $\overrightarrow{MC}$ | D. | $\overrightarrow{MD}$ |
11.命题“y=f(x)(x∈M)是奇函数”的否定是( )
| A. | ?x∈M,f(-x)=-f(x) | B. | ?x∈M,f(-x)≠-f(x) | C. | ?x∈M,f(-x)=-f(x) | D. | ?x∈M,f(-x)≠-f(x) |
8.(2+x)(1-2x)5展开式中,x2项的系数为( )
| A. | 30 | B. | 70 | C. | 90 | D. | -150 |
9.在△ABC中,AB=5,AC=12,BC=13,一只小蚂蚁从△ABC的内切圆的圆心处开始随机爬行,当蚂蚁(在三角形内部)与△ABC各边距离不低于1个单位时其行动是安全的,则这只小蚂蚁在△ABC内任意行动时安全的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |