题目内容
9.在△ABC中,角A、B、C所对的边分别为a、b、c,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$=2,那么c=2.分析 可画出图形,进行数量积的运算便可由$\overrightarrow{AB}•\overrightarrow{AC}=\overrightarrow{BA}•\overrightarrow{BC}=2$得到bccosA=accosB=2,由正弦定理即可得出A=B,进而得到a=b,然后由余弦定理,根据bccosA=2即可求出c的值.
解答 解:如图,
∵$\overrightarrow{AB}•\overrightarrow{AC}=\overrightarrow{BA}•\overrightarrow{BC}=2$;
∴bccosA=accosB=2;
∴bcosA=acosB;
根据正弦定理,b=2RsinB,a=2RsinA,代入上式:2RsinBcosA=2RcosBsinA;
∴sinBcosA=cosBsinA;
∴sin(B-A)=0;
∵A,B∈(0,π);
∴A=B;
∴a=b
由余弦定理,$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{c}{2b}$,代入bccosA=2得:$bc•\frac{c}{2b}=2$;
∴c2=4;
∴c=2.
故答案为:2.
点评 考查了数量积的计算公式,以及正余弦定理,等腰三角形的概念.

练习册系列答案
相关题目
1.已知函数f(x)=loga(6-ax)在(-3,2)上是减函数,则a的取值范围是( )
| A. | (0,3) | B. | (1,3] | C. | (1,3) | D. | [3,+∞) |
2.曲线的参数方程为$\left\{\begin{array}{l}x=1+2cosθ\\ y=2+3sinθ\end{array}\right.(θ为参数)$,则该曲线的普通方程为( )
| A. | $\frac{{{{(x+1)}^2}}}{4}-\frac{{{{(y+2)}^2}}}{9}=1$ | B. | $\frac{{{{(x-1)}^2}}}{4}-\frac{{{{(y-2)}^2}}}{9}=1$ | C. | $\frac{{{{(x+1)}^2}}}{4}+\frac{{{{(y+2)}^2}}}{9}=1$ | D. | $\frac{{{{(x-1)}^2}}}{4}+\frac{{{{(y-2)}^2}}}{9}=1$ |
19.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾天气的主要原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
(Ⅰ)分别求这两年样本数据的中位数和平均值,并以此推断2016年11月~12月的空气质量是否比2015年同期有所提高?
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.
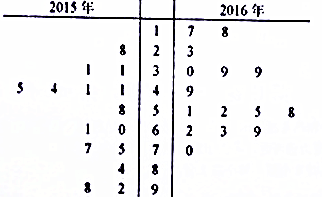
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.

4.某学校拟安排6名教师在元旦期间(2016年12月31日至2017年1月2日)值班,每天安排2人,每人值班1天,若6名教师中的甲12月31日不值班,乙1月2日不值班,则不同的安排方法共有( )
| A. | 30种 | B. | 36种 | C. | 42种 | D. | 48种 |
14.直线a∥平面α,直线b⊥平面α,则直线a与直线b的位置关系为( )
| A. | 异面 | B. | 垂直 | ||
| C. | 平行 | D. | 平行或异面或相交 |
19.观察下列等式:
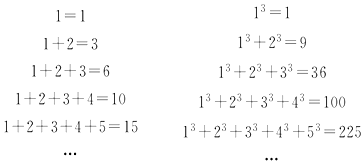
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
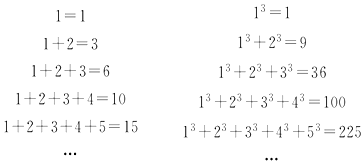
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |