题目内容
10.已知f(x)=x3+ax2+bx,在x=1处有极值-2,则a+2b=-6.分析 求出函数的导数,得到关于a,b的方程组,求出a,b的值,从而求出a+2b的值即可.
解答 解:f′(x)=3x2+2ax+b,
由f(x)=x3+ax2+bx,在x=1处有极值-2,
得$\left\{\begin{array}{l}{f(1)=1+a+b=-2}\\{f′(1)=3+2a+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=0}\\{b=-3}\end{array}\right.$,
故a+2b=-6,
故答案为:-6.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
2.曲线的参数方程为$\left\{\begin{array}{l}x=1+2cosθ\\ y=2+3sinθ\end{array}\right.(θ为参数)$,则该曲线的普通方程为( )
| A. | $\frac{{{{(x+1)}^2}}}{4}-\frac{{{{(y+2)}^2}}}{9}=1$ | B. | $\frac{{{{(x-1)}^2}}}{4}-\frac{{{{(y-2)}^2}}}{9}=1$ | C. | $\frac{{{{(x+1)}^2}}}{4}+\frac{{{{(y+2)}^2}}}{9}=1$ | D. | $\frac{{{{(x-1)}^2}}}{4}+\frac{{{{(y-2)}^2}}}{9}=1$ |
15.函数f(x)=x3-ax+100在区间(1,+∞)内是增函数,则实数a的取值范围是( )
| A. | a<3 | B. | a>3 | C. | a≤3 | D. | a≥3 |
19.观察下列等式:
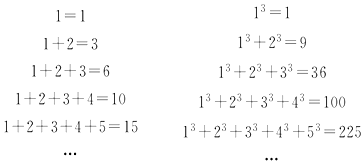
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
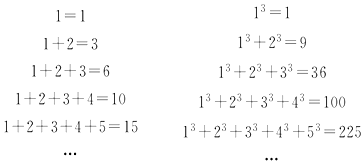
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |