题目内容
8．（2+x）（1-2x）5展开式中，x2项的系数为（ ）| A． | 30 | B． | 70 | C． | 90 | D． | -150 |
分析 先求得（1-2x）5展开式的通项公式，可得（2+x）（1-2x）5展开式中，x2项的系数．
解答 解：∵（1-2x）5展开式的通项公式为Tr+1=C5r•（-2x）r，
∴（2+x）（1-2x）5展开式中，x2项的系数为2C52•（-2）2+C51•（-2）=70，
故选：B．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于中档题．
练习册系列答案
相关题目
19．观察下列等式：
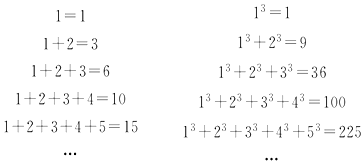
可以推测：13+23+33+…+n3=________（n∈N*，用含n的代数式表示）．（ ）
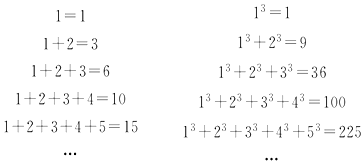
可以推测：13+23+33+…+n3=________（n∈N*，用含n的代数式表示）．（ ）
| A． | $\frac{1}{4}{n^2}{（n-1）^2}$ | B． | $\frac{1}{4}{n^2}{（n-2）^2}$ | C． | $\frac{1}{4}{n^2}{（n+1）^2}$ | D． | $\frac{1}{4}{n^2}{（n+2）^2}$ |
16．从装有3个红球和2个白球的袋中任取3个球，则所取的3个球中至少有2个红球的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{5}$ | C． | $\frac{7}{10}$ | D． | $\frac{3}{5}$ |
17．
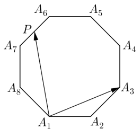如图所示，正八边形A1A2A3A4A5A6A7A8的边长为2，若P为该正八边形边上的动点，则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为（ ）
如图所示，正八边形A1A2A3A4A5A6A7A8的边长为2，若P为该正八边形边上的动点，则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为（ ）| A． | $[0，8+6\sqrt{2}]$ | B． | $[-2\sqrt{2}，8+6\sqrt{2}]$ | C． | $[-8-6\sqrt{2}，2\sqrt{2}]$ | D． | $[-8-6\sqrt{2}，8+6\sqrt{2}]$ |
18．在△ABC中，角A，B，C所对的边分别是a，b，c，若a2+b2=2c2，则角C的取值范围是（ ）
| A． | $（{0，\frac{π}{3}}]$ | B． | $（{0，\frac{π}{3}}）$ | C． | $（{0，\frac{π}{6}}]$ | D． | $（{0，\frac{π}{6}}）$ |