题目内容
14.数列{an}的前n项和为Sn.若数列{an}的各项按如下规则排列:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{1}{4}$,$\frac{2}{4}$,$\frac{3}{4}$,$\frac{1}{5}$,$\frac{2}{5}$,$\frac{3}{5}$,$\frac{4}{5}$…$\frac{1}{n}$,$\frac{2}{n}$,…$\frac{n-1}{n}$…若存在正整数k,使Sk-1<10,Sk>10,则ak=$\frac{6}{7}$.分析 把原数列划分,发现他们的个数是1,2,3,4,5…构建新数列bn,很显然是个等差数列,利用等差数列的和知道T5=$\frac{15}{2}$,T6=$\frac{21}{2}$,所以ak定在$\frac{1}{7}$,$\frac{2}{7}$,…,$\frac{6}{7}$中,在根据Sk-1<10,Sk≥10求出具体结果.
解答 解:把原数列分组,分母相同的为一组,发现他们的个数是1,2,3,4,5…
构建新数列{bn},表示数列中每一组的和,则bn=$\frac{n}{2}$是个等差数列,记{bn}的前n项和为Tn,
利用等差数列的和知道T5=$\frac{15}{2}$,T6=$\frac{21}{2}$,
所以ak定在$\frac{1}{7}$,$\frac{2}{7}$,…,$\frac{6}{7}$中,
又因为Sk-1<10,Sk≥10,而T5+$\frac{1}{7}$+$\frac{2}{7}$+…+$\frac{5}{7}$=9+$\frac{9}{14}$<10,T5+$\frac{1}{7}$+$\frac{2}{7}$+…+$\frac{5}{7}$+$\frac{6}{7}$=10+$\frac{1}{2}$>10,
故第k项为ak=$\frac{6}{7}$.
故答案为$\frac{6}{7}$.
点评 本题目主要考查学生对数列的观察能力,找出数列之间的相互关系,根据等差数列的前n项和计算公式,根据已有条件计算.考查学生的计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
4.某学校拟安排6名教师在元旦期间(2016年12月31日至2017年1月2日)值班,每天安排2人,每人值班1天,若6名教师中的甲12月31日不值班,乙1月2日不值班,则不同的安排方法共有( )
| A. | 30种 | B. | 36种 | C. | 42种 | D. | 48种 |
19.观察下列等式:
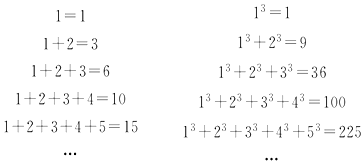
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
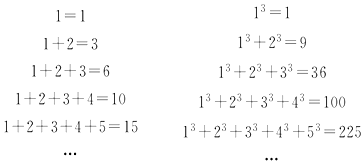
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |
