题目内容
11.命题“y=f(x)(x∈M)是奇函数”的否定是( )| A. | ?x∈M,f(-x)=-f(x) | B. | ?x∈M,f(-x)≠-f(x) | C. | ?x∈M,f(-x)=-f(x) | D. | ?x∈M,f(-x)≠-f(x) |
分析 根据命题的否定命题的解答办法,解得即可.
解答 解:命题“y=f(x)(x∈M)是奇函数”的否定,?x∈M,f(-x)≠-f(x),
故选:D.
点评 本题考查命题的否定,解题的关键是掌握并理解命题否定的书写方法规则,书写时注意量词的变化.

练习册系列答案
相关题目
19.观察下列等式:
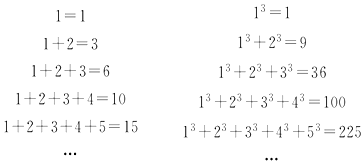
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
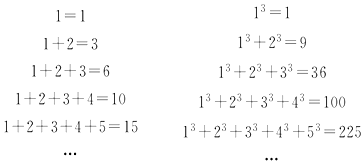
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |
16.从装有3个红球和2个白球的袋中任取3个球,则所取的3个球中至少有2个红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{5}$ |
1.已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=4|$\overrightarrow{b}$|.设$\overrightarrow{b}$与$\overrightarrow{b}$-$\overrightarrow{a}$的夹角为θ,则cosθ=( )
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $-\frac{{\sqrt{15}}}{4}$ |
