题目内容
7.已知函数$f(x)=lg\frac{1+ax}{1-2x}$是定义在(-b,b)上的奇函数,(a,b∈R且a≠-2),则ab的取值范围是( )| A. | $({1,\sqrt{2}}]$ | B. | $({0,\sqrt{2}}]$ | C. | $({1,\sqrt{2}})$ | D. | $({0,\sqrt{2}})$ |
分析 先由奇函数的性质求a,从而求得其定义域,再用(-b,b)是定义域的子集求得b的范围,从而求得ab的取值范围.
解答 解:∵$f(x)=lg\frac{1+ax}{1-2x}$是奇函数,
∴f(-x)=-f(x),
解得a=2
∴f(x)=lg$\frac{1+2x}{1-2x}$,
其定义域是(-$\frac{1}{2}$,$\frac{1}{2}$)
∴0<b≤$\frac{1}{2}$,
∴1<ab≤$\sqrt{2}$,
故选:A
点评 本题主要考查函数的奇偶性及定义域优先原则.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾天气的主要原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
(Ⅰ)分别求这两年样本数据的中位数和平均值,并以此推断2016年11月~12月的空气质量是否比2015年同期有所提高?
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.
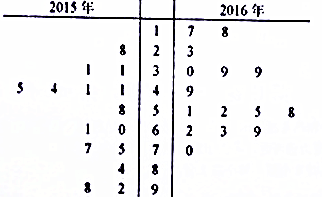
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.

15.函数f(x)=x3-ax+100在区间(1,+∞)内是增函数,则实数a的取值范围是( )
| A. | a<3 | B. | a>3 | C. | a≤3 | D. | a≥3 |
12.点P(x,y)是直线kx+y+3=0上一动点,PA,PB是圆C:x2+y2-4y=0的两条切线,A,B是切点,若四边形PACB面积的最小值为2,则k的值为( )
| A. | $2\sqrt{2}$ | B. | $±2\sqrt{2}$ | C. | 2 | D. | ±2 |
19.观察下列等式:
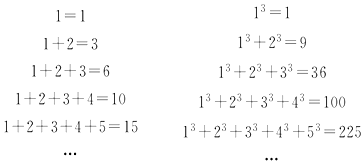
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
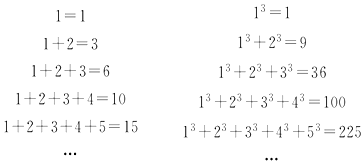
可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).( )
| A. | $\frac{1}{4}{n^2}{(n-1)^2}$ | B. | $\frac{1}{4}{n^2}{(n-2)^2}$ | C. | $\frac{1}{4}{n^2}{(n+1)^2}$ | D. | $\frac{1}{4}{n^2}{(n+2)^2}$ |
16.从装有3个红球和2个白球的袋中任取3个球,则所取的3个球中至少有2个红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{5}$ |
17.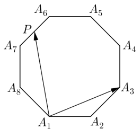 如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
 如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )| A. | $[0,8+6\sqrt{2}]$ | B. | $[-2\sqrt{2},8+6\sqrt{2}]$ | C. | $[-8-6\sqrt{2},2\sqrt{2}]$ | D. | $[-8-6\sqrt{2},8+6\sqrt{2}]$ |