题目内容

若x=
π
12
，则sin4x-cos4x的值为（　　）
A、
1
2
B、-
1
2
C、-
3
2
D、
3
2
考点：二倍角的余弦
专题：三角函数的求值
分析：利用平方差公式、二倍角的余弦公式，把要求的式子化为-cos2x，从而利用条件求得结果．
解答： 解：∵x=
π
12
，
∴sin4x-cos4x=sin2x-cos2x=-cos2x=-cos
π
6
=-
3
2
，
故选：C．
点评：本题主要考查二倍角的余弦公式的应用，属于基础题．
练习册系列答案
相关题目
已知a，b，c∈R，下列命题中正确的是（　　）
A、a＞b⇒ac2＞bc2
B、ac2＞bc2⇒a＞b
C、a3＞b3⇒
1
a
＜
1
b
D、a2＞b2⇒a＞|b|
在小于100的自然数中，所有被7除余2的数之和为（　　）
A、765B、665
C、763D、663
已知P、M、N是单位圆上互不相同的三个点，且满足|
PM
|=|
PN
|，则
PM
•
PN
的最小值是 （　　）
A、-
1
4
B、-
1
2
C、-
3
4
D、-1
函数y=
sinx
的定义域为（　　）
A、[0，π]
B、x为第Ⅰ、Ⅱ象限的角
C、{x|2kπ≤x≤（2k+1）π，k∈z}
D、（0，π）
函数y=
1
2
sin（2x-
π
3
）的图象可以看作是把函数y=
1
2
sin2x的图象（　　）
A、向左平移
π
3
得到的
B、向右平移
π
6
得到的
C、向右平移
π
12
得到的
D、向左平移
π
6
得到的
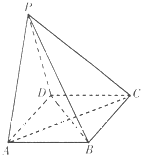如图，在四棱锥P-ABCD中，底面四边形ABCD为矩形，PA=PD，AD=
2
AB=2，且平面PAD⊥平面.4BCD．
（Ⅰ）求证：PC⊥BD；
（Ⅱ）若四棱锥P-ABCD的体积为
4
2
3
，求二面角A-PC-D的余弦值．
某同学在研究性学习中，了解到淘宝网站一批发店铺在今年的前五个月的销售量（单位：百件）的数据如表：
月份x12345
销售量y（百件）44566
（Ⅰ）该同学为了求出y关于x的回归方程
y
=
b
x+
a
，根据表中数据已经正确算出
b
=0.6，试求出
?
a
的值，并估计该店铺6月份的产品销售量；（单位：百件）
（Ⅱ）一零售商现存有从该淘宝批发店铺2月份进货的4件和3月份进货的5件产品，顾客甲现从该零售商处随机购买了3件，后经了解，该淘宝批发店铺今年2月份的产品都有质量问题，而3月份的产品都没有质量问题．记顾客甲所购买的3件产品中存在质量问题的件数为X，求X的分布列和数学期望．
从某校高三年级随机抽取一个班，对该班50名学生的高校招生体检表中的视力情况进行统计，其频率分布直方图如图所示．若某高校A专业对视力的要求在0.9以上，则该班学生中能报A专业的人数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网