题目内容
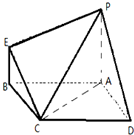如图：ABCD是平行四边形，AP⊥平面ABCD，BE∥AP，AB=AP=2，BE=BC=1，∠CBA=60°（1）求证：EC∥平面PAD；
（2）求证：平面PAC⊥平面EBC；
（3）求直线PC与平面PABE所成角的正弦值．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由已知条件推导出平面PAD∥平面EBC，由此能证明EC∥平面PAD．
（2）由余弦定理得AC=
，由勾股定理得AC⊥BC，由线面垂直得BE⊥AC，由此能证明平面BEC⊥平面PAC．
（3）作CH⊥AB于H，连结PH，由题设知∠HPC即为线面角，由此能求出直线PC与平面PABE所成角的正弦值．
（2）由余弦定理得AC=
| 3 |
（3）作CH⊥AB于H，连结PH，由题设知∠HPC即为线面角，由此能求出直线PC与平面PABE所成角的正弦值．
解答：
（1）证明：因为BE∥PA，
BE?平面PAD，PA?平面PAD，
所以BE∥平面PAD，同理BC∥平面PAD，
所以平面PAD∥平面EBC，
因为EC?平面EBC，所以EC∥平面PAD…（4分）
（2）证明：因为AB=2，BC=1，∠CBA=60°，
由余弦定理得，AC=
，
所以由勾股定理逆定理∠BCA=90°，
所以AC⊥BC，又因为BE⊥平面ABCD，所以BE⊥AC，
则有AC⊥平面EBC，AC?平面PAC
所以平面BEC⊥平面PAC．…（8分）
（3）解：作CH⊥AB于H，连结PH，
又因为CH⊥PA，所以CH⊥平面PABE，
所以∠HPC即为线面角，
∴sin∠HPC=
=
．…（13分）
BE?平面PAD，PA?平面PAD，
所以BE∥平面PAD，同理BC∥平面PAD，
所以平面PAD∥平面EBC，
因为EC?平面EBC，所以EC∥平面PAD…（4分）
（2）证明：因为AB=2，BC=1，∠CBA=60°，
由余弦定理得，AC=
| 3 |
所以由勾股定理逆定理∠BCA=90°，
所以AC⊥BC，又因为BE⊥平面ABCD，所以BE⊥AC，
则有AC⊥平面EBC，AC?平面PAC
所以平面BEC⊥平面PAC．…（8分）
（3）解：作CH⊥AB于H，连结PH，
又因为CH⊥PA，所以CH⊥平面PABE，
所以∠HPC即为线面角，
∴sin∠HPC=
| HC |
| PC |
| ||
| 14 |
点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，考查直线与平面所成角的正弦值的求法，解题时要注意空间思维能力的培养．
练习册系列答案
快捷英语周周练系列答案
相关题目
如图，在直平行六面体ABCD-A1B1C1D1中，侧棱AA1=3，AB=3，BC=
在四棱锥P-ABCD中，AB∥DC，AB⊥平面PAD，PD=AD，AB=2DC，E是PB的中点．求证：