题目内容
己知各项均为正数的数列{an}满足:a1=3,且anan+12-2(an2-1)an+1-an=0,n∈N*.
(1)设bn=an-
,求数列{bn}的通项公式;
(2)设Sn=a12+a22+…+an2,Tn=
+
+…+
,求Sn+Tn,并确定最小正整数n,使Sn+Tn为整数.
(1)设bn=an-
| 1 |
| an |
(2)设Sn=a12+a22+…+an2,Tn=
| 1 |
| a12 |
| 1 |
| a22 |
| 1 |
| an2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题意知,bn+1=an+1-
=
=
=2(an-
)=2bn,由此求出bn=
.
(2)由(1)有Sn+Tn=(a1-
)2+(a2-
)2+…+(an-
)2+2n=
(4n-1)+2n,n∈N*,为使Sn+Tn=
(4n-1)2+2n,n∈N*,当且仅当
为整数.由此能求出n的最小值为9.
| 1 |
| an+1 |
| an+12-1 |
| an+1 |
| 2(an2-1) |
| an |
| 1 |
| an |
| 2n+2 |
| 3 |
(2)由(1)有Sn+Tn=(a1-
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 64 |
| 27 |
| 64 |
| 27 |
| 4n-1 |
| 27 |
解答:
解:(1)由题意知,
bn+1=an+1-
=
=
=2(an-
)=2bn,
b1=a1-
=
,
∴数列{bn}是公比为2,首项为
的等比数列,其通项公式为bn=
.
(2)由(1)有Sn+Tn=(a1-
)2+(a2-
)2+…+(an-
)2+2n
=(
)2+(
)2+…(
)2+2n
=
(4n-1)+2n,n∈N*,
为使Sn+Tn=
(4n-1)2+2n,n∈N*,当且仅当
为整数.
当n=1,2时,Sn+Tn不为整数,
当n≥3时,4n-1=(1+3)n-1=
×3+
×32+33(
+…+3n-3
),
∴只需
=
•
为整数,
∵3n-1与3互质,∴为9的整数倍,
当n=9时,
•
=13为整数,
故n的最小值为9.
bn+1=an+1-
| 1 |
| an+1 |
| an+12-1 |
| an+1 |
| 2(an2-1) |
| an |
| 1 |
| an |
b1=a1-
| 1 |
| a1 |
| 8 |
| 3 |
∴数列{bn}是公比为2,首项为
| 8 |
| 3 |
| 2n+2 |
| 3 |
(2)由(1)有Sn+Tn=(a1-
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
=(
| 23 |
| 3 |
| 24 |
| 3 |
| 2n+2 |
| 3 |
=
| 64 |
| 27 |
为使Sn+Tn=
| 64 |
| 27 |
| 4n-1 |
| 27 |
当n=1,2时,Sn+Tn不为整数,
当n≥3时,4n-1=(1+3)n-1=
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
∴只需
3
| ||||
| 27 |
| n |
| 9 |
| 3n-1 |
| 2 |
∵3n-1与3互质,∴为9的整数倍,
当n=9时,
| n |
| 9 |
| 3n-1 |
| 2 |
故n的最小值为9.
点评:本题考查数列的通项公式的求法,考查实数的最小值的求法,解题时要认真审题,注意二项式定理的合理运用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
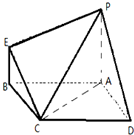 如图:ABCD是平行四边形,AP⊥平面ABCD,BE∥AP,AB=AP=2,BE=BC=1,∠CBA=60°
如图:ABCD是平行四边形,AP⊥平面ABCD,BE∥AP,AB=AP=2,BE=BC=1,∠CBA=60°