题目内容
已知函数f(x)=-
x2+(a+1)x-alnx,当a>0时,求f(x)的单调区间.
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出函数的导数,再分别讨论①0<a<1时②a>1时的情况,从而求出其单调区间.
解答:
解:∵f′(x)=-x+(a+1)-
,
①0<a<1时,
令f′(x)>0⇒(x-a)(x-1)<0,
解得:a<x<1,
令f′(x)<0⇒(x-a)(x-1)>0,
解得:x>1,0<x<a,
∴f(x)在(a,1)上递增,在(0,a),(1,+∞)上递减,
②a>1时,
令f′(x)>0⇒(x-a)(x-1)<0,
解得:1<x<a,
令f′(x)<0⇒(x-a)(x-1)>0,
解得:x>a,0<x<1,
∴f(x)在(1,a)递增,在(0,1),(a,+∞)递减.
③a=1时,f(x)=-(x+
)+2≤0,
∴f(x)在(0,+∞)上单调递减.
| a |
| x |
①0<a<1时,
令f′(x)>0⇒(x-a)(x-1)<0,
解得:a<x<1,
令f′(x)<0⇒(x-a)(x-1)>0,
解得:x>1,0<x<a,
∴f(x)在(a,1)上递增,在(0,a),(1,+∞)上递减,
②a>1时,
令f′(x)>0⇒(x-a)(x-1)<0,
解得:1<x<a,
令f′(x)<0⇒(x-a)(x-1)>0,
解得:x>a,0<x<1,
∴f(x)在(1,a)递增,在(0,1),(a,+∞)递减.
③a=1时,f(x)=-(x+
| 1 |
| x |
∴f(x)在(0,+∞)上单调递减.
点评:本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道基础题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则这个几何体的体积为( )


A、
| ||
B、
| ||
| C、8 | ||
D、
|
若P的Q的北偏东44°50′,则Q在P的( )
| A、东偏北45°10′ |
| B、东偏北45°50′ |
| C、南偏西44°50′ |
| D、西偏南45°50′ |
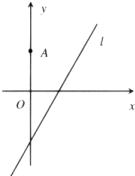 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.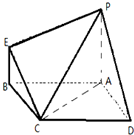 如图:ABCD是平行四边形,AP⊥平面ABCD,BE∥AP,AB=AP=2,BE=BC=1,∠CBA=60°
如图:ABCD是平行四边形,AP⊥平面ABCD,BE∥AP,AB=AP=2,BE=BC=1,∠CBA=60°