题目内容
在等差数列{an}中，an＞0，a1+a2≤4，a2+a5≤12，则a3的取值范围为 ．
考点：简单线性规划的应用,等差数列的性质
专题：直线与圆
分析：利用已知条件判断公差的范围，然后求解a3的取值范围．
解答：
解：在等差数列{an}中，an＞0，所以公差d＞0，
a1+a2≤4，a2+a5≤12，
可得0＜2a1+d≤4，0＜2a1+5d≤12，
a1+2d=u（2a1+d）+v（2a1+5d），
可得
，解得
，a1+2d=
（2a1+d）+
（2a1+5d）∈（0，5]，
∴a3=a1+2d∈（0，5]．
故答案为：（0，5]．
a1+a2≤4，a2+a5≤12，
可得0＜2a1+d≤4，0＜2a1+5d≤12，
a1+2d=u（2a1+d）+v（2a1+5d），
可得
|
|
| 1 |
| 8 |
| 3 |
| 8 |
∴a3=a1+2d∈（0，5]．
故答案为：（0，5]．
点评：本题考查等差数列的基本性质的应用，线性规划的应用，推理以及计算能力．
练习册系列答案
阅读快车系列答案
相关题目
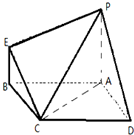如图：ABCD是平行四边形，AP⊥平面ABCD，BE∥AP，AB=AP=2，BE=BC=1，∠CBA=60°已知点A（1，2），B（3，1），则直线AB的斜率为（ ）
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |