题目内容
12.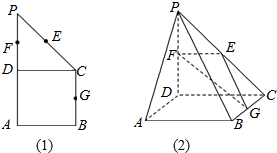 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).(1)求证:平面EFG∥平面PAB;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
分析 (1)证明EF∥AB.利用直线与平面平行的判定定理证明EF∥平面PAB.然后利用平面与平面平行的判定定理证明平面EFG∥平面PAB.
(2)连接DE,EQ,证明PD⊥AD,AD⊥PC.推出DE⊥PC,利用直线与平面垂直的判定定理证明PC⊥平面ADQ.
(3)利用等体积VC-EFG=VG-CEF,转化求解即可.
解答  解:(1)证明:∵E、F分别是PC,PD的中点,
解:(1)证明:∵E、F分别是PC,PD的中点,
∴EF∥CD
又CD∥AB.∴EF∥AB.
∵EF?平面PAB,AB?平面PAB,
∴EF∥平面PAB.
同理,EG∥平面PAB,∵EF∩EG=E,EF?平面EFG,EG?平面EFG
∴平面EFG∥平面PAB. …(4分)
(2)解:连接DE,EQ,
∵E、Q分别是PC、PB的中点,∴EQ∥BC,又 BC∥AD.
∴EQ∥AD
∵平面PDC⊥平面ABCD,PD⊥DC,∴PD⊥平面ABCD.∴PD⊥AD,
又AD⊥DC,PD∩DC=D∴AD⊥平面PDC,∴AD⊥PC.
在△PDC中,PD=CD,E是PC的中点,∴DE⊥PC,
∵DE∩AD=D∴PC⊥平面ADEQ,即PC⊥平面ADQ. …(8分)
(3)VC-EFG=VG-CEF=$\frac{1}{3}$S△CEF•GC=$\frac{1}{3}$×($\frac{1}{2}$×1×1)×1=$\frac{1}{6}$.…(12分)
点评 本题考查直线与平面垂直的判定定理以及平面与平面平行的判定定理,几何体的体积的求法,考查空间想象能力以及计算能力,转化思想的应用.

练习册系列答案
相关题目
3.已知倾斜角为θ的直线,与直线x-3y+1=0垂直,则$\frac{2}{{3{{sin}^2}θ-{{cos}^2}θ}}$=( )
| A. | $\frac{10}{3}$ | B. | 一$\frac{10}{3}$ | C. | $\frac{10}{13}$ | D. | 一$\frac{10}{13}$ |
20.点P在边长为2的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
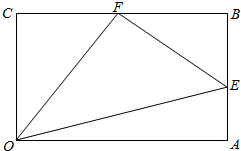 如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.
如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.