题目内容
1.设$f(x)=kx+m,g(x)=lnx-\frac{1}{x}$.(1)若函数f(x)-g(x)在区间(0,+∞)上减函数,求k的取值范围;
(2)当k=2时,若函数f(x)的图象是函数g(x)的图象的切线,求m的值.
分析 (1)由题意可得f′(x)-g′(x)≤0在区间(0,+∞)上恒成立.即k≤$\frac{1}{x}$+$\frac{1}{{x}^{2}}$(x>0)恒成立,有二次函数的值域,即可得到所求k的范围;
(2)由题意可得y=2x+m为g(x)=lnx-$\frac{1}{x}$的切线,设切点为(x0,y0),求出导数,切线的斜率,解方程可得切点,进而得到m的值.
解答 解:(1)函数f(x)-g(x)在区间(0,+∞)上减函数,
即为f′(x)-g′(x)≤0在区间(0,+∞)上恒成立.
即k≤$\frac{1}{x}$+$\frac{1}{{x}^{2}}$(x>0)恒成立,
由$\frac{1}{x}$+$\frac{1}{{x}^{2}}$=($\frac{1}{x}$+$\frac{1}{2}$)2-$\frac{1}{4}$>0,可得k≤0,
即有k的取值范围(-∞,0];
(2)由题意可得y=2x+m为g(x)=lnx-$\frac{1}{x}$的切线,
设切点为(x0,y0),g′(x)=$\frac{1}{x}$+$\frac{1}{{x}^{2}}$,
即有$\frac{1}{{x}_{0}}$+$\frac{1}{{{x}_{0}}^{2}}$=2,解得x0=1(负的舍去),
y0=ln1-1=-1,
即有m=y0-2x0=-1-2=-3.
点评 本题考查导数的运用:求切线的斜率和单调性,考查不等式恒成立问题的解法,注意运用参数分离,考查运算能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
13.如果集合A={x|x=2kπ+π,k∈Z},B={x|x=4kπ+π,k∈Z},则( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=ϕ |
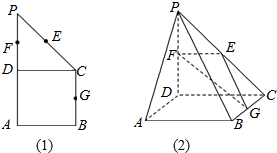 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)). 如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,