题目内容
4.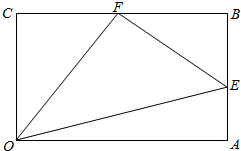 如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.
如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.(1)试用解析式将y表示成x的函数;
(2)求三角形池塘OEF面积S的最小值及此时x的值.
分析 (1)由∠EOF=$\frac{π}{4}$,可得∠COF+∠AOE=$\frac{π}{4}$,则tan(∠COF+∠AOE)=$\frac{\frac{x}{4}+\frac{y}{5}}{1-\frac{xy}{20}}$=1,化简可得函数的解析式,由0≤y≤4求得x的范围;
(2)三角形池塘OEF面积S=S矩形OABC-S△AOE-S△COF-S△BEF,运用三角形的面积公式,设t=x+4,求得S的表达式,运用基本不等式可得最小值和x的值.
解答 解:(1)由∠EOF=$\frac{π}{4}$,可得∠COF+∠AOE=$\frac{π}{4}$,
即有tan∠COF=$\frac{x}{4}$,tan∠AOE=$\frac{y}{5}$,
则tan(∠COF+∠AOE)=$\frac{\frac{x}{4}+\frac{y}{5}}{1-\frac{xy}{20}}$=1,
即有y=$\frac{5(4-x)}{4+x}$,由y≤4,解得x≥$\frac{4}{9}$,
则函数的解析式为y=$\frac{5(4-x)}{4+x}$,($\frac{4}{9}$≤x≤4);
(2)三角形池塘OEF面积S=S矩形OABC-S△AOE-S△COF-S△BEF
=4×5-$\frac{1}{2}$×5y-$\frac{1}{2}$×4x-$\frac{1}{2}$×(4-y)(5-x)
=20-$\frac{1}{2}$•$\frac{25(4-x)}{4+x}$-2x-$\frac{1}{2}$(5-x)•$\frac{9x-4}{x+4}$
=20+$\frac{5{x}^{2}-40x-80}{2(x+4)}$($\frac{4}{9}$≤x≤4),
令t=x+4($\frac{40}{9}$≤t≤8),
即有S=20+$\frac{1}{2}$(5t+$\frac{160}{t}$-80)
≥20+$\frac{1}{2}$(2$\sqrt{5t•\frac{160}{t}}$-80)=20$\sqrt{2}$-20.
当且仅当5t=$\frac{160}{t}$即t=4$\sqrt{2}$,此时x=4$\sqrt{2}$-4,
△OEF的面积取得最小值,且为20$\sqrt{2}$-20.
点评 本题考查函数的解析式的求法,注意运用两角和的正切公式,考查三角形的面积的最小值,注意运用间接法求面积,再由换元法和基本不等式,属于中档题.

| A. | 向右平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=ϕ |
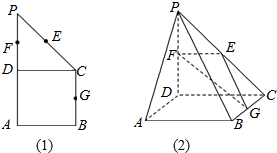 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).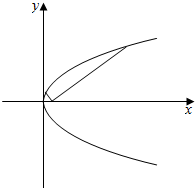 已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).
已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6). 如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,