题目内容
17.已知{an}为等差数列,且a4=8,a3+a7=20.(1)求数列{an}的通项公式an;
(2)设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,求数列{bn}的前n项和Sn.
分析 (1)利用等差数列的通项公式即可得出;
(2)利用“裂项求和”即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a4=8,a3+a7=20,
∴$\left\{\begin{array}{l}{{a}_{1}+3d=8}\\{2{a}_{1}+8d=20}\end{array}\right.$,解得a1=d=2.
∴an=2+2(n-1)=2n
(2)${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{2n•2(n+1)}$=$\frac{1}{4}$$(\frac{1}{n}-\frac{1}{n+1})$,
∴数列{bn}的前n项和Sn=$\frac{1}{4}[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$]
=$\frac{1}{4}$$(1-\frac{1}{n+1})$
=$\frac{n}{4n+4}$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.下列集合中表示同一集合的是( )
| A. | M={整数},N={整数集} | B. | M={(3,2)},N={(2,3)} | ||
| C. | M={(x,y)|x+y=1},N={(y,x)|x+y=1} | D. | M={1,2},N={(1,2)} |
2.已知b<a<0,$\root{3}{a}$-$\root{3}{b}$=m,$\root{3}{a-b}$=n,则有( )
| A. | m>n | B. | m<n | C. | m=n | D. | m≤n |
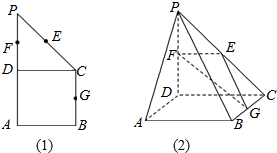 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)). 如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,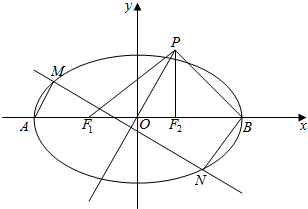 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别是F1,F2,左、右顶点分别为A、B,焦距为2c,O为坐标原点,点P(c,b)满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别是F1,F2,左、右顶点分别为A、B,焦距为2c,O为坐标原点,点P(c,b)满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$.