题目内容
3.已知倾斜角为θ的直线,与直线x-3y+1=0垂直,则$\frac{2}{{3{{sin}^2}θ-{{cos}^2}θ}}$=( )| A. | $\frac{10}{3}$ | B. | 一$\frac{10}{3}$ | C. | $\frac{10}{13}$ | D. | 一$\frac{10}{13}$ |
分析 直线x-3y+1=0的斜率=$\frac{1}{3}$,因此与此直线垂直的直线的斜率k=-3.可得tanθ=-3.再利用同角三角函数基本关系式即可得出.
解答 解:直线x-3y+1=0的斜率=$\frac{1}{3}$,因此与此直线垂直的直线的斜率k=-3.
∴tanθ=-3.
∴$\frac{2}{{3{{sin}^2}θ-{{cos}^2}θ}}$=$\frac{2(si{n}^{2}θ+co{s}^{2}θ)}{3si{n}^{2}θ-co{s}^{2}θ}$=$\frac{2(ta{n}^{2}θ+1)}{3ta{n}^{2}θ-1}$=$\frac{2({3}^{2}+1)}{3×{3}^{2}-1}$=$\frac{10}{13}$.
故选:C.
点评 本题考查了相互垂直的直线斜率之间的关系、同角三角函数基本关系式、“弦化切”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.要得到函数y=-cos2x的图象,只需将函数y=sin(2x-$\frac{π}{4}$)的图象( )
| A. | 向右平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
13.如果集合A={x|x=2kπ+π,k∈Z},B={x|x=4kπ+π,k∈Z},则( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=ϕ |
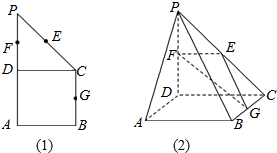 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).