题目内容
已知z1,z2∈C,设A:z12+z22=0,B:z1,z2全为零,则A是B的( )
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:令Z1=1,Z2=i,我们可以判断出“Z12+Z22=0⇒Z1=0且Z2=0”的真假,进而再判断出“Z1=0且Z2=0⇒Z12+Z22=0”的真假,结合必要条件、充分条件与充要条件的判断方法,即可得到答案.
解答:
解:令Z1=1,Z2=i,则Z12+Z22=0成立,而Z1=0且Z2=0不成立,
即Z12+Z22=0⇒Z1=0且Z2=0为假命题;
而当Z1=0且Z2=0时,Z12+Z22=0成立,
即Z1=0且Z2=0⇒Z12+Z22=0为真命题;
故Z12+Z22=0是Z1=0且Z2=0的必要非充分条件,
故选B
即Z12+Z22=0⇒Z1=0且Z2=0为假命题;
而当Z1=0且Z2=0时,Z12+Z22=0成立,
即Z1=0且Z2=0⇒Z12+Z22=0为真命题;
故Z12+Z22=0是Z1=0且Z2=0的必要非充分条件,
故选B
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
y=sin(2x-
)-sin2x的一个单调递增区间是( )
| π |
| 3 |
A、[-
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
“B=60°”是“△ABC三个内角成等差数列”的( )
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、既不充分又非必要条件. |
如图,已知AB⊥平面BCD,BC⊥CD,则图中直角三角形的个数为( )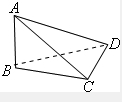

| A、1 | B、2 | C、3 | D、4 |
已知直角三角形的周长为定值2l,则它的面积的最大值为( )
A、2
| ||
B、3
| ||
C、(3+2
| ||
D、(3-2
|
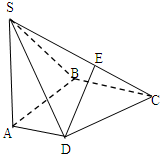 四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求:
四棱锥S-ABCD中,底面ABCD为直角梯形,AB垂直于AD和BC,SA⊥面ABCD,SA=AB=BC=2,AD=1.求: