题目内容

3．已知函数f（x）=lnx-x3与g（x）=x3-ax的图象上存在关于x轴的对称点，则a的取值范围为（　　）
A．（-∞，e）B．（-∞，e]C．（-∞，$\frac{1}{e}$）D．（-∞，$\frac{1}{e}$]

分析 由题意可知f（x）=-g（x）有解，即y=lnx与y=ax有交点，根据导数的几何意义，求出切点，结合图象，可知a的范围．

解答 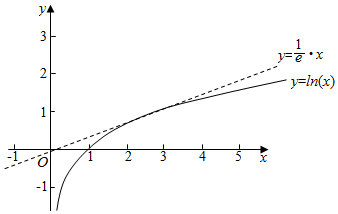解：函数f（x）=lnx-x3与g（x）=x3-ax的图象上存在关于x轴的对称点，
∴f（x）=-g（x）有解，
∴lnx-x3=-x3+ax，
∴lnx=ax，在（0，+∞）有解，
分别设y=lnx，y=ax，
若y=ax为y=lnx的切线，
∴y′=$\frac{1}{x}$，
设切点为（x0，y0），
∴a=$\frac{1}{{x}_{0}}$，ax0=lnx0，
∴x0=e，
∴a=$\frac{1}{e}$，
结合图象可知，a≤$\frac{1}{e}$
故选：D．

点评 本题导数的几何意义，以及函数值的问题，关键是转化为y=lnx与y=ax有交点，属于中档题．

练习册系列答案
相关题目
13．根据我国发布的《环境空气质量指数AQI技术规定》（试行），AQI共分为六级：[0，50）为优，[50，100）为良，[100，150）为轻度污染，[150，200）为重度污染，[200，250），[250，300）均为重度污染，300及以上为严重污染．某市2015年11月份30天的AQI的频率分布直方图如图所示．
（1）该市11月份环境空气质量优或良共有多少天？
（2）若采用分层抽样方法从30天中抽取10天进行市民户外晨练人数调查，则重度污染被抽到的天数共有多少天？
（3）空气质量指数低于150时市民适宜户外晨练，该市民王先生决定某天早晨进行户外晨练，则他当天适宜户外晨练的概率是多少？
14．某商场举行购物抽奖活动，抽奖箱中放有编号分别为1，2，3，4，5的五个小球，小球除编号不同外，其余均相同．
活动规则如下：从抽奖箱中随机抽取一球，若抽到的小球编号为3，则获得奖金100元；若抽到的小球编号为偶数，则获得奖金50元；若抽到其余编号的小球，则不中奖．现某顾客依次有放回的抽奖两次．
（I）求该顾客两次抽奖后都没有中奖的概率；
（Ⅱ）求该顾客两次抽奖后获得奖金之和为100元的概率．
11．若函数y=f（x），x∈A满足：?x1，x2∈A，（x1-x2）[f（x1）-f（x2）]≤0恒成立，则称函数y=f（x）为定义在A上的“非增函数”，若函数f（x）是区间[0，1]上的“非增函数”，且f（0）=1，f（x）+f（1-x）=1，又当x∈[0，$\frac{1}{4}$]时，f（x）≤-2x+1恒成立，有下列命题：①?x∈（0，1]，f（x）≥0；②若x1，x2∈[0，1]，且x1≠x2，则f（x1）≠f（x2）；③f（$\frac{1}{8}$）+f（$\frac{5}{11}$）+f（$\frac{7}{13}$）+f（$\frac{7}{8}$）=2．其中正确的是（　　）
A．①②B．②③C．①③D．①②③
18．已知函数f（x）=|x-3|，g（x）=-|x+4|+2m．
（1）当a＞0时，求关于x的不等式f（x）+1-a＞0（a∈R）的解集；
（2）若函数f（x）的图象恒在函数g（x）图象的上方，求m的取值范围．
8．某农户承包了一块苹果园，每年投入成本为10000元，苹果产量和市场价格均具有随机性，且互不影响，根据多年统计数据进行分析，其产量和市场价格如表：
产量（kg） 40005000 
 概率 0.50.5
苹果的市场价格（元/千克） 8 10
 概率 0.40.6
（1）设X表示这个果园每年的利润，求X的分布列和期望；
（2）求3年中至少有2年的利润不少于30000元的概率．
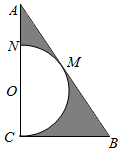15．如图所示，△ABC中，∠C=90°，∠B=60°，AB=2$\sqrt{3}$，在三角形内挖去半圆（圆心O在边AC上，半圆与BC、AB相切于点C、M，与AC交于N），则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$．
12．设$f（x）=\left\{\begin{array}{l}x-2\;，x≥5\\ f[{f（x+6）}]，x＜5\end{array}\right.$，则f（1）=3．
13．已知集合M={x|x＜0}，N={x|x2-x-2＜0}，则M∩N=（　　）
A．{x|-1＜x＜0}B．{x|-2＜x＜0}C．{x|x＜2}D．{x|x＜1}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网