题目内容
13. 根据我国发布的《环境空气质量指数AQI技术规定》(试行),AQI共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为重度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2015年11月份30天的AQI的频率分布直方图如图所示.
根据我国发布的《环境空气质量指数AQI技术规定》(试行),AQI共分为六级:[0,50)为优,[50,100)为良,[100,150)为轻度污染,[150,200)为重度污染,[200,250),[250,300)均为重度污染,300及以上为严重污染.某市2015年11月份30天的AQI的频率分布直方图如图所示.(1)该市11月份环境空气质量优或良共有多少天?
(2)若采用分层抽样方法从30天中抽取10天进行市民户外晨练人数调查,则重度污染被抽到的天数共有多少天?
(3)空气质量指数低于150时市民适宜户外晨练,该市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
分析 (1)由频率分布直方图能求出该市11月环境空气质量优或良的天数.
(2)由频率分布直方图能求出重度污染被抽到的天数.
(3)设“市民王先生当天适宜户外晨练”为事件A,由频率分布直方图能求出他当天适宜户外晨练的概率.
解答 解:(1)由题意得该市11月环境空气质量优或良共有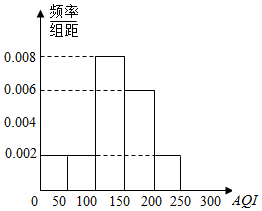
(0.002+0.002)×50×30=6(天).
(2)重度污染被抽到的天数共有0.06×50×10=3(天).
(3)设“市民王先生当天适宜户外晨练”为事件A,
则P(A)=(0.002+0.002+0.008)×50=0.6.
点评 本题考查频率分直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的合理运用.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
1.为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如表所示,经计算K2=7.822,则环保知识是否优秀与性别有关的把握为( )
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}{n}_{+2}}$
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.500 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
8.等比数列{an}的前n项和为Sn,已知S4=a2+a3+9a1,a5=32,则a1=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
18.计算:cos24°cos36°-cos66°cos54°=( )
| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
5.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}+2x,x≤0\\ ln(x+1),x>0\end{array}\right.$,若对x∈R都有|f(x)|≥ax,则实数a的取值范围是( )
| A. | (-∞,0] | B. | [-2,0] | C. | [-2,1] | D. | (-∞,1] |
3.已知函数f(x)=lnx-x3与g(x)=x3-ax的图象上存在关于x轴的对称点,则a的取值范围为( )
| A. | (-∞,e) | B. | (-∞,e] | C. | (-∞,$\frac{1}{e}$) | D. | (-∞,$\frac{1}{e}$] |