题目内容
18.已知函数f(x)=|x-3|,g(x)=-|x+4|+2m.(1)当a>0时,求关于x的不等式f(x)+1-a>0(a∈R)的解集;
(2)若函数f(x)的图象恒在函数g(x)图象的上方,求m的取值范围.
分析 (1)对参数a进行分类讨论,分别解不等式即可;
(2)函数f(x)的图象恒在函数g(x)图象的上方,可转化为不等式|x-3|+|x+4|>2m恒成立,利用不等式的性质求出|x-3|+|x+4|的最小值,就可以求出m的范围.
解答 解:(1)当a>0时,由f(x)+1-a>0得|x-3|+1-a>0,
即|x-3|>a-1,
若a-1<0,即0<a<1时,不等式的解集是R,
若a-1≥0,即a≥1时,由|x-3|>a-1得x-3>a-1或x-3<-(a-1),
即x>a+2或x<4-a.
所以,当0<a<1时,不等式的解集为R;
当a≥1时,不等式的解集为(-∞,4-a)∪(a+2,+∞).
(2))∵f(x)=|x-3|,g(x)=-|x+4|+2m,函数f(x)的图象恒在函数g(x)图象的上方,
∴f(x)≥g(x)恒成立,
即|x-3|≥-|x+4|+2m恒成立,
即|x-3|+|x+4|≥2m恒成立,
∵|x-3|+|x+4|≥|-4-3|=7,
则2m≤7,则m≤$\frac{7}{2}$.
∴m的取值范围为:m≤$\frac{7}{2}$.
点评 本题考查绝对值不等式的解法,分类讨论的方法,以及不等式的性质,涉及面较广,知识性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.等比数列{an}的前n项和为Sn,已知S4=a2+a3+9a1,a5=32,则a1=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
3.已知函数f(x)=lnx-x3与g(x)=x3-ax的图象上存在关于x轴的对称点,则a的取值范围为( )
| A. | (-∞,e) | B. | (-∞,e] | C. | (-∞,$\frac{1}{e}$) | D. | (-∞,$\frac{1}{e}$] |
8.已知e为自然对数的底数,若对任意的x∈[0,1],总存在唯一的y∈[-1,1],使得x+y2ey-a=0成立,则实数a的取值范围是( )
| A. | [1,e] | B. | $(1+\frac{1}{e},e]$ | C. | (1,e] | D. | $[1+\frac{1}{e},e]$ |
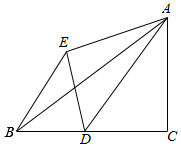 如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.