题目内容
9.已知等差数列{an}中,a1=1,且a1,a2,a4+2成等比数列.(1)求数列{an}的通项公式及其前n项和Sn;
(2)设${b_n}={2^{{{({-1})}^n}{a_n}}}$,求数列{bn}的前n项和Tn.
分析 (1)设等差数列{an}的公差为d,由a1=1,且a1,a2,a4+2成等比数列.可得:${a}_{2}^{2}$=a1•(a4+2),即(1+d)2=1×(1+3d+2),解得d.经过验证可得d,再利用等差数列的通项公式与求和公式即可得出.
(2)${b_n}={2^{{{({-1})}^n}{a_n}}}$=${2}^{(-1)^{n}(2n-1)}$.当n为偶数时,$\frac{{b}_{n+2}}{{b}_{n}}$=$\frac{{2}^{2n+3}}{{2}^{2n-1}}$=16.当n为奇数时,$\frac{{b}_{n+2}}{{b}_{n}}$=$\frac{{2}^{-(2n+3)}}{{2}^{-(2n-1)}}$=$\frac{1}{16}$.可得数列{bn}的奇数项是以$\frac{1}{2}$为首项,$\frac{1}{16}$为公比的等比数列;偶数项是以8为首项,16为公比的等比数列.利用求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a1=1,且a1,a2,a4+2成等比数列.
∴${a}_{2}^{2}$=a1•(a4+2),即(1+d)2=1×(1+3d+2),解得d=2或-1.
其中d=-1时,a2=0,舍去.
∴d=2,可得an=1+2(n-1)=2n-1.
Sn=$\frac{n(1+2n-1)}{2}$=n2.
(2)${b_n}={2^{{{({-1})}^n}{a_n}}}$=${2}^{(-1)^{n}(2n-1)}$.
∴当n为偶数时,$\frac{{b}_{n+2}}{{b}_{n}}$=$\frac{{2}^{2n+3}}{{2}^{2n-1}}$=16.当n为奇数时,$\frac{{b}_{n+2}}{{b}_{n}}$=$\frac{{2}^{-(2n+3)}}{{2}^{-(2n-1)}}$=$\frac{1}{16}$.
∴数列{bn}的奇数项是以$\frac{1}{2}$为首项,$\frac{1}{16}$为公比的等比数列;偶数项是以8为首项,16为公比的等比数列.
∴数列{bn}的前2n项和T2n=(b1+b3+…+b2n-1)+(b2+b4+…+b2n)
=$\frac{\frac{1}{2}×[1-(\frac{1}{16})^{n}]}{1-\frac{1}{16}}$+$\frac{8×(1{6}^{n}-1)}{16-1}$
=$\frac{8}{15}$(16n-16-n).
点评 本题考查了等差数列与等比数列的定义通项公式与求和公式及其性质、分组求和方法,考查了推理能力与计算能力,属于中档题.


| A. | 6+4$\sqrt{2}$ | B. | 4+4$\sqrt{2}$ | C. | 2 | D. | 8 |
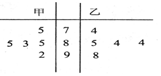 如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )| A. | x1<x2,y1<y2 | B. | x1<x2,y1>y2 | C. | x1>x2,y1>y2 | D. | x1>x2,y1<y2 |
| 不关注 | 关注 | 总计 | |
| 男生 | 30 | 15 | 45 |
| 女生 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 0.10 | B. | 0.05 | C. | 0.025 | D. | 0.01 |
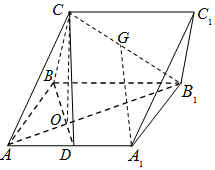 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.