题目内容
13.学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:| 不关注 | 关注 | 总计 | |
| 男生 | 30 | 15 | 45 |
| 女生 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 0.10 | B. | 0.05 | C. | 0.025 | D. | 0.01 |
分析 根据表中数据计算统计量K2,参考临界数据,即可得出结论.
解答 解:根据表中数据,计算统计量
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{100{×(30×10-45×15)}^{2}}{75×25×45×55}$≈3.03>2.706,
参考临界数据知,认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,
此结论出错的概率不超过0.10.
故选:A.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.定义在R上的函数y=f(x)满足:f(x)+f'(x)>1,f(0)=2018,则不等式exf(x)-ex>2017(其中e为自然对数的底数)的解集为( )
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
1.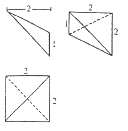 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $2\sqrt{3}$ |
2.在△ABC中,a,b,c分别是内角A,B,C的对边,若A=$\frac{2π}{3}$,b=$\sqrt{2}$,△ABC的面积为$\sqrt{3}$,则a的值为( ) )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{14}$ |