题目内容
20.已知下列命题:①?x∈(0,2),3x>x3的否定是:?x∈(0,2),3x≤x3;
②若f(x)=2x-2-x,则?x∈R,f(-x)=-f(x);
③若f(x)=x+$\frac{1}{x+1}$,?x0∈(0,+∞),f(x0)=1;
④在△ABC中,若A>B,则sin A>sin B.
其中真命题是①②④.(将所有真命题序号都填上)
分析 利用命题的否定判断①的正误;函数的奇偶性判断②的正误;方程的解判断③的正误;三角形中碳钢正弦定理判断④的正误;
解答 解:对于①?x∈(0,2),3x>x3的否定是:?x∈(0,2),3x≤x3;满足命题的否定形式,正确;
②若f(x)=2x-2-x,则?x∈R,f(-x)=2-x-2x=-(2x-2-x)=-f(x);函数是奇函数,正确;
③若f(x)=x+$\frac{1}{x+1}$,x+$\frac{1}{x+1}$=1,可得x2+x+1=x+1,解得x=0,所以?x0∈(0,+∞),f(x0)=1;不正确;
④在△ABC中,若A>B,则sin A>sin B.在三角形中大角对大边,∵A>B,∴a>b,由正弦定理可得
从而a=2RsinA,b=2RsinB,∴2RsinA>2RsinB,∴sinA>sinB.所以④正确.
故答案为:①②④.
点评 本题考查命题的真假的判断与应用,考查命题的否定函数的奇偶性,解三角形,是基本知识的考查.

练习册系列答案
相关题目
15.已知等差数列{an}的a1=-20,公差为d,前n项和为Sn,则“3<d<5”是“Sn的最小值仅为S6”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.定义在R上的函数y=f(x)满足:f(x)+f'(x)>1,f(0)=2018,则不等式exf(x)-ex>2017(其中e为自然对数的底数)的解集为( )
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
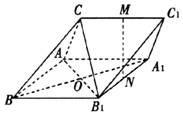 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.