题目内容
15.已知函数f(x)=ln(1+x)-ln(1-x).(1)判断函数f(x)的奇偶性;
(2)解关于x的方程f(x)=1.
分析 (1)先确定函数的定义域,再运用奇偶性的定义判断函数为奇函数;
(2)先将方程式化简,把问题你等价为$\frac{1+x}{1-x}$=e,解出即可.
解答 解:(1)∵f(x)=ln(1+x)-ln(1-x),
∴函数的定义域为:(-1,1),
且f(-x)=ln(1-x)-ln(1+x)=-f(x),
所以,f(x)为奇函数;
(2)由f(x)=ln$\frac{1+x}{1-x}$=1得,
$\frac{1+x}{1-x}$=e,解得,x=$\frac{e-1}{e+1}$,
即该方程的解为:x=$\frac{e-1}{e+1}$.
点评 本题主要考查了函数奇偶性的判断和对数方程的解法,涉及对数的运算法则和对数函数的图象与性质,属于中档题.

练习册系列答案
相关题目
10.函数f(x)=$\left\{\begin{array}{l}{lnx,x>0}\\{-\frac{1}{2}x+1,x≤0}\end{array}\right.$,则f[f(2-2e)]的值是( )
| A. | e | B. | $\frac{1}{e}$ | C. | 1 | D. | -1 |
20.若将函数y=sin(ωx+$\frac{π}{4}$)(ω>0)向左平移$\frac{π}{6}$个单位长度后,与函数y=cos(ωx+$\frac{π}{4}$)的图象重合,则ω的最小值为3.
6.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长、短轴长、焦距成等差数列,则椭圆的离心率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
 (3)请认真阅读下列程序框图:已知程序框图
(3)请认真阅读下列程序框图:已知程序框图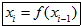 中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}
中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}