题目内容
5. (3)请认真阅读下列程序框图:已知程序框图
(3)请认真阅读下列程序框图:已知程序框图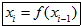 中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}
中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}(Ⅰ)若输入${x_0}=\frac{49}{65}$,请写出数列{xn}的所有项;
(Ⅱ)若输出的无穷数列{xn}是一个常数列,试求输入的初始值x0的值;
(Ⅲ)若输入一个正数x0时,产生的数列{xn}满足:任意一项xn,都有xn<xn+1,试求正数x0的取值范围.
分析 (Ⅰ)根据f(x)解析式确定出D,把x0=$\frac{49}{65}$代入程序框图中计算,得到xi∉D时,确定出数列{xn}的所有项即可;
(Ⅱ)根据输出的无穷数列{xn}是一个常数列,确定出输入的初始值x0的值即可;
(Ⅲ)根据题意列出不等式,根据正数x0,求出解集,确定出正数x0的取值范围即可.
解答 解:(Ⅰ)当x0=$\frac{49}{65}$时,x1=f($\frac{49}{65}$)=$\frac{11}{19}$,x2=f($\frac{11}{19}$)=$\frac{1}{5}$,x3=f($\frac{1}{5}$)=-1,
则输出的数列为{$\frac{11}{19}$,$\frac{1}{5}$,-1};
(Ⅱ)数列{xn}是一个常数列,则有x1=x2=…=xn=x0,即x0=f(x0)=$\frac{4{x}_{0}-2}{{x}_{0}-1}$,
解得:x0=1或x0=2,
则输入的初始值x0为1或2时输出的为常数列;
(Ⅲ)由题意知:xn+1=f(xn)=$\frac{4{x}_{n}-2}{{x}_{n}+1}$>xn,
∵x0>0,∴xn>0,有$\frac{4{x}_{n}-2}{{x}_{n}+1}$>xn,
得4xn-2>xn(xn+1),即xn2-3xn+2<0,即(xn-2)(xn-1)<0,
有xn+1>xn,须(x0-2)(x0-1)<0,
解得:1<x0<2,
则当正数x0在(1,2)内取值时,所输出的数列{xn}对任意正整数n满足xn<xn+1.
点评 此题考查了程序框图,弄清程序框图中的运算程序是解本题的关键.

练习册系列答案
相关题目
15.定义点P(x0,y0)到直线l:ax+by+c=0(a2+b2≠0)的有向距离为d=$\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$.已知点P1、P2到直线l的有向距离分别是d1、d2.以下命题正确的是( )
| A. | 若d1-d2=0,则直线P1P2与直线l平行 | |
| B. | 若d1+d2=0,则直线P1P2与直线l平行 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2<0,则直线P1P2与直线l相交 |
16.下列命题正确的是( )
| A. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| B. | “am2<bm2”是”a<b”的必要不充分条件 | |
| C. | 命题p:存在x0∈R,使得x02+x0+1<0,则¬p:任意x∉R,都有x2+x+1≥0 | |
| D. | 命题“若x2<1,则-1<x<1”的逆否命题是若x≥1或x≤-1,则x2≥1 |
10.P、Q分别为3x+4y-12=0与6x+8y+1=0上任一点,则|PQ|的最小值为( )
| A. | $\frac{13}{5}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 6 |