题目内容
6.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长、短轴长、焦距成等差数列,则椭圆的离心率是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 根据椭圆的长轴长、短轴长、焦距成等差数列,建立几何量之间的关系,即可求得离心率.
解答 解:由题意,椭圆的长轴长、短轴长、焦距成等差数列,
∴4b=2c+2a
∴2b=c+a
∴4b2=c2+2ac+a2
∴3a2-2ac-5c2=0
∴5e2+2e-3=0
∴(e+1)(5e-3)=0
∴e=$\frac{3}{5}$.
故选:A.
点评 本题考查椭圆的几何性质,解题的关键是根据椭圆的焦距、短轴长、长轴长成等差数列,建立几何量之间的关系.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
1.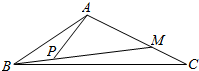 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )| A. | -2 | B. | 2 | C. | $\frac{2}{3}$ | D. | $-\frac{11}{3}$ |
15.不等式2x-3y-5≥0表示的平面区域是( )
| A. |  | B. |  | C. |  | D. |  |
16.若正四面体ABCD的棱长为1,则它的外接球体积为( )
| A. | $\frac{\sqrt{6}}{8}$π | B. | $\frac{3}{2}$π | C. | $\frac{\sqrt{6}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |