题目内容
11.已知函数f(x)=($\frac{1}{3}$x3-x2+$\frac{2}{3}$)cos2017($\frac{π}{3}x$+$\frac{2π}{3}$)+2x+3在[-2015,2017]上的最大值为M,最小值为m,则M+m=( )| A. | 5 | B. | 10 | C. | 1 | D. | 0 |
分析 f(x)=$\frac{1}{3}(x-1)[(x-1)^{2}-3]co{s}^{2017}[π+\frac{π}{3}(x-1)]$+2x+3=-$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(x-1)+5,令g(x)=-$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(x-1),g(x)+g(2-x)=)═-$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(x-1)+$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(1-x)=0,所以函数g(x)的图象关于点(1,0)对称,得M+m=10.
解答 解:∵f(x)=$\frac{1}{3}(x-1)[(x-1)^{2}-3]co{s}^{2017}[π+\frac{π}{3}(x-1)]$+2x+3=-$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(x-1)+5.
令g(x)=-$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(x-1),
g(x)+g(2-x)=)═-$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(x-1)+$\frac{1}{3}$(x-1)[(x-1)2-3]cos($\frac{π}{3}(x-1)$)+2(1-x)=0,
所以函数g(x)的图象关于点(1,0)对称,
∴函数g(x)在[-2015,2017]上的最大值为M1,最小值为m1,M1+m1=0.
M=M1+5,最小值为m=m1+5.则M+m=10.
故选:B
点评 本题考查了函数对称性质与值域的转化关系,考查了推理能力与计算能力,属于难题.

| A. | θ=$\frac{π}{6}$ | B. | θ=$\frac{7}{6}$π | C. | θ=$\frac{π}{6}$和θ=$\frac{7}{6}$π | D. | θ=$\frac{5}{6}$π |
| A. | [$\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
| A. | (-1,1) | B. | (-2,-1) | C. | (-2,1) | D. | (1,2) |
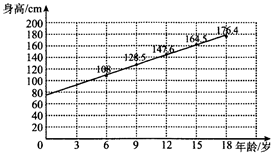 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )| A. | 据样本数据估计,该地区青少年身高与年龄成正相关 | |
| B. | 所抽取数据中,5000名青少年平均身高约为145cm | |
| C. | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D. | 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |