题目内容
3.从1,2,3,4,5这五个数中一次随机取两个数,则取出的两个数的和为奇数的概率为$\frac{3}{5}$.分析 先求出基本事件总数n=${C}_{5}^{2}=10$,再求出取出的两个数的和为奇数包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}=6$,由此能求出取出的两个数的和为奇数的概率.
解答 解:从1,2,3,4,5这五个数中一次随机取两个数,
基本事件总数n=${C}_{5}^{2}=10$,
取出的两个数的和为奇数包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}=6$,
∴取出的两个数的和为奇数的概率p=$\frac{m}{n}=\frac{6}{10}=\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
13.观察数列1,2,2,3,3,3,8,8,8,…的特点,按此规律,则第100项为( )
| A. | 213 | B. | 214 | C. | 215 | D. | 216 |
14.将一个大正方形平均分成9个小正方形,向大正方形区域随机投掷一个点(每次都能投中),投中最左侧三个小正方形区域的事件记为A,投中最上面三个小正方形区域或正中间的一个小正方形区域的事件记为B,则P(A|B)=( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
12.直线$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.(t$为参数)与圆$\left\{\begin{array}{l}x=4+2cosφ\\ y=2sinφ\end{array}\right.(φ$为参数)相切,则此直线的倾斜角$α({α>\frac{π}{2}})$等于( )
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
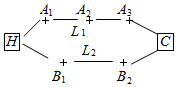 如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.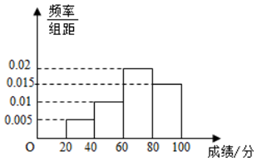 随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.
随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.