题目内容
1.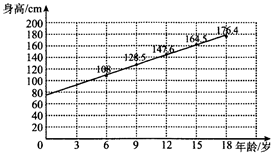 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )| A. | 据样本数据估计,该地区青少年身高与年龄成正相关 | |
| B. | 所抽取数据中,5000名青少年平均身高约为145cm | |
| C. | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D. | 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |
分析 根据散点图与线性回归方程的意义,对选项中的命题进行分析、判断正误即可.
解答 解:对于A,根据样本数据的回归直线从左向右是上升的,
估计该地区青少年身高与年龄成正相关,正确;
对于B,计算平均数为$\frac{1}{5}$×(108+128.5+147.6+164.5+176.4)=145,
估计这5000名青少年平均身高约为145cm,正确;
对于C,根据回归直线的意义知,
直线L的斜率的值近似等于样本中青少年平均身高每年的增量,正确;
对于D,根据回归直线的定义知,回归直线必过样本数据的中心点,
不是必过某些数据的中心点,D错误.
故选:D.
点评 本题考查了散点图与线性回归方程的应用问题,是基础题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
12.直线$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.(t$为参数)与圆$\left\{\begin{array}{l}x=4+2cosφ\\ y=2sinφ\end{array}\right.(φ$为参数)相切,则此直线的倾斜角$α({α>\frac{π}{2}})$等于( )
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
16.某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
表2
已知表1数据的中位数估计值为26,回答以下问题.
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
表1
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
6.第96届(春季)全国糖酒商品交易会于2017年3月23日至25日在四川举办.展馆附近一家川菜特色餐厅为了研究参会人数与本店所需原材料数量的关系,在交易会前查阅了最近5次交易会的参会人数x(万人)与餐厅所用原材料数量y(袋),得到如下数据:
(Ⅰ)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$))
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$))
10.二元线性方程组$\left\{\begin{array}{l}{x+5y=0}\\{2x+3y=4}\end{array}\right.$的系数矩阵D=( )
| A. | $(\begin{array}{l}{0}&{5}\\{3}&{4}\end{array})$ | B. | $(\begin{array}{l}{1}&{0}\\{2}&{3}\end{array})$ | C. | $(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$ | D. | $(\begin{array}{l}{1}&{0}\\{2}&{4}\end{array})$ |
19. 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图):
(1)试根据频率分布直方图估计小区平均每户居民的平均损失;
(同一组中的数据用该组区间的中点值作代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过6000元的居民中随机抽出2户进行捐款援助,求抽出的2户居民损失均超过8000元的概率;
(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,在图2表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关?
附:临界值参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图):(1)试根据频率分布直方图估计小区平均每户居民的平均损失;
(同一组中的数据用该组区间的中点值作代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过6000元的居民中随机抽出2户进行捐款援助,求抽出的2户居民损失均超过8000元的概率;
(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,在图2表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关?
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | ||
| 捐款不超过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
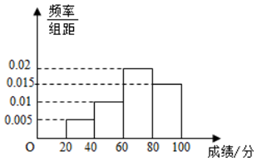 随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.
随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.