题目内容
19.已知a>0,且a≠1,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{a})^{x}-1,x≤0}\\{{x}^{2}+(4a-1)x+3a-1,x>0}\end{array}\right.$在R上单调递增,且关于x的方程|f(x)|=x+1恰有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{1}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
分析 由题意可知f(x)在两段上均为增函数,且f(x)在(0,+∞)上的最小值大于或等于f(0),作出|f(x)|和y=x+1的图象,根据交点个数判断3a与2的大小关系,列出不等式组解出.
解答 解:∵f(x)是R上的单调递增函数,
∴y=x2+(4a-1)x+3a-1在(0,+∞)上单调递增,y=($\frac{1}{a}$)x-1在(-∞,0]上单调递增,
且f(x)在(0,+∞)上的最小值大于或等于f(0).
即$\left\{\begin{array}{l}{\frac{1}{a}>1}\\{\frac{1-4a}{2}≤0}\\{3a-1≥0}\end{array}\right.$解得$\frac{1}{3}≤a<1$,
作出y=|f(x)|和y=x+1的函数草图如图所示:
由图象可知|f(x)|=x+1在(-∞,0)上有且只有一解,
∵|f(x)|=x+1恰有两个不相等的实数解,
∴x2+(4a-1)x+3a-1=x+1在(0,+∞)上只有1解,
即x2+(4a-2)x+3a-2=0在(0,+∞)上只有1解,
$\left\{\begin{array}{l}{△=(4a-2)^{2}-4(3a-2)=0}\\{-\frac{4a-2}{2}>0}\end{array}\right.$或$\left\{\begin{array}{l}{△=(4a-2)^{2}-4(3a-2)>0}\\{3a-2<0}\end{array}\right.$
解得a$<\frac{2}{3}$.
综上,a的取值范围是:[$\frac{1}{3}$,$\frac{2}{3}$),
故选:B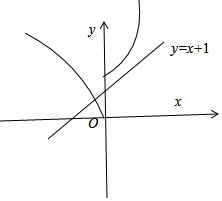
点评 本题考查了分段函数的单调性,函数零点的个数判断,结合函数图象判断端点值的大小是关键,属于中档题.

练习册系列答案
相关题目
7.根据如下样本数据
得到的回归方程为$\widehaty=\hat bx+\hat a$,则( )
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 4.1 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | $\hat a>0,\hat b>0$ | B. | $\hat a>0,\hat b<0$ | C. | $\hat a<0,\hat b>0$ | D. | $\hat a<0,\hat b<0$ |
14.将一个大正方形平均分成9个小正方形,向大正方形区域随机投掷一个点(每次都能投中),投中最左侧三个小正方形区域的事件记为A,投中最上面三个小正方形区域或正中间的一个小正方形区域的事件记为B,则P(A|B)=( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
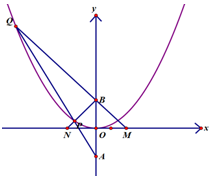 已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.
已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ=$\frac{2π}{3}$.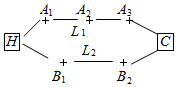 如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.