题目内容
20.已知集合M={x|x2+x-2<0},N={x|x+1<0},则M∩N=( )| A. | (-1,1) | B. | (-2,-1) | C. | (-2,1) | D. | (1,2) |
分析 运用二次不等式和一次不等式的解法,化简集合M,N,再由交集的定义,即可得到所求.
解答 解:集合M={x|x2+x-2<0}={x|(x+2)(x-1)<0}={x|-2<x<1},
N={x|x+1<0}={x|x<-1},
可得M∩N={x|-2<x<-1},
故选:B.
点评 本题考查集合的运算,主要是交集的求法,注意运用定义法,同时考查二次不等式和一次不等式的解法,以及运算能力,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
12.直线$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.(t$为参数)与圆$\left\{\begin{array}{l}x=4+2cosφ\\ y=2sinφ\end{array}\right.(φ$为参数)相切,则此直线的倾斜角$α({α>\frac{π}{2}})$等于( )
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
10.二元线性方程组$\left\{\begin{array}{l}{x+5y=0}\\{2x+3y=4}\end{array}\right.$的系数矩阵D=( )
| A. | $(\begin{array}{l}{0}&{5}\\{3}&{4}\end{array})$ | B. | $(\begin{array}{l}{1}&{0}\\{2}&{3}\end{array})$ | C. | $(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$ | D. | $(\begin{array}{l}{1}&{0}\\{2}&{4}\end{array})$ |
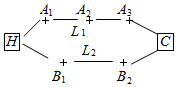 如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
如图,李先生家住H小区,他工作在C处科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为$\frac{1}{2}$;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.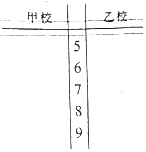 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下: