题目内容
二面角α-l-β的棱l上有一点P,射线PA在α内,且与棱l成45°角,与面β成30°角则二面角α-l-β的大小为( )
| A、30°或150° |
| B、45°或135° |
| C、60°或120° |
| D、90° |
考点:二面角的平面角及求法
专题:综合题,空间角
分析:求二面角平面角的大小,关键是找(作出)出二面角的平面角,本题可以利用定义法寻找.过点P作平面β的垂线PB,垂足为B,过点B作BC垂直于l,连接PC,根据条件可以证得∠PCB为二面角α-l-β的平面角,再分别在△PBA,△PCA,△PCB中,可求二面角α-l-β的平面角.
解答:
解:过点P作平面β的垂线PB,垂足为B,过点B作BC垂直于l,连接PC
∵PB⊥β,l?β,∴PB⊥l
∵l⊥BC,∴∠PCB为二面角α-l-β的平面角
设PB=1,在△PBA中,∠PAB=30°,∴PA=2
在△PCA中,∠PAC=45°,∴PC=
在△PCB中,PB=1,PC=
,∴∠PCB=45°,
∴二面角α-l-β的大小为45°或135°.
故选:B.
∵PB⊥β,l?β,∴PB⊥l
∵l⊥BC,∴∠PCB为二面角α-l-β的平面角
设PB=1,在△PBA中,∠PAB=30°,∴PA=2
在△PCA中,∠PAC=45°,∴PC=
| 2 |
在△PCB中,PB=1,PC=
| 2 |
∴二面角α-l-β的大小为45°或135°.
故选:B.
点评:本题的考点是二面角的平面角及求法,主要考查利用定义找(作出)出二面角的平面角,关键是找(作出)出二面角的平面角,同时也考查学生计算能力.一般地,二面角的平面角的求法,遵循一作、二证、三求的步骤,定义法事最基本的寻找方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把11 011(2)化为十进制数为( )
| A、11 | B、31 | C、27 | D、19 |
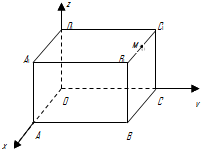 如图所示的空间直角坐标系O-xyz下,长方体OABC-D1A1B1C1中,|OA|=3,|OC|=4,|OD1|=2,则B1C1的中点M的坐标是( )
如图所示的空间直角坐标系O-xyz下,长方体OABC-D1A1B1C1中,|OA|=3,|OC|=4,|OD1|=2,则B1C1的中点M的坐标是( )A、(
| ||
| B、(3,2,2) | ||
| C、(3,4,1) | ||
D、(
|
下列命题正确的个数是①
+
=
②
•
=
③
-
=
④0•
=0( )
| AB |
| BA |
| 0 |
| 0 |
| AB |
| 0 |
| AB |
| AC |
| BC |
| AB |
| A、1 | B、2 | C、3 | D、4 |
数列{an}的前n项和Sn与通项公式an满足关系式Sn=nan+2n2-2n(n∈N*),则a100-a10=( )
| A、-90 | B、-180 |
| C、-360 | D、-400 |