题目内容
设a,b∈R,定义在区间(b,3b-a)上的函数f(x)=
是奇函数,
(1)求b的值;
(2)判断函数f(x)的单调性,并证明之;
(3)解关于x的不等式:f(2x-
)+f(
)<f(0).
2x+
| ||
| 2x+1 |
(1)求b的值;
(2)判断函数f(x)的单调性,并证明之;
(3)解关于x的不等式:f(2x-
| 1 |
| 2 |
| 1 |
| 4 |
考点:奇偶性与单调性的综合,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)根据函数奇偶性的定义和性质即可求b的值;
(2)利用指数函数的单调性即可判断函数f(x)的单调性;
(3)根据函数的奇偶性和单调性将不等式进行化简即可得到结论.
(2)利用指数函数的单调性即可判断函数f(x)的单调性;
(3)根据函数的奇偶性和单调性将不等式进行化简即可得到结论.
解答:
解:(1)∵函数是定义在区间(b,3b-a)上的奇函数,
∴f(0)=0,b+3b-a=4b-a=0,
则f(0)=
=0,即1+
=0,解得a=-2.
则b=-
.
(2)∵a=-2.
∴f(x)=
=
,定义域为(-
,
),
则f(x)为增函数:
证明:f(x)=
=
=1-
,
∵当x∈(-
,
)时,2x+1为增函数,
为减函数,则-
为增函数,
∴1-
为增函数,即f(x)为增函数.
(3)∵f(0)=0,
∴不等式:f(2x-
)+f(
)<f(0)等价为不等式f(2x-
)<-f(
)=f(-
).
∵f(x)在(-
,
)为增函数,
∴
,即
,
则
,解得x<-2.
∴f(0)=0,b+3b-a=4b-a=0,
则f(0)=
1+
| ||
| 2 |
| a |
| 2 |
则b=-
| 1 |
| 2 |
(2)∵a=-2.
∴f(x)=
2x+
| ||
| 2x+1 |
| 2x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
则f(x)为增函数:
证明:f(x)=
| 2x-1 |
| 2x+1 |
| 2x+1-2 |
| 2x+1 |
| 2 |
| 2x+1 |
∵当x∈(-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
∴1-
| 2 |
| 2x+1 |
(3)∵f(0)=0,
∴不等式:f(2x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∵f(x)在(-
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
|
则
|
点评:本题主要考查函数奇偶性和单调性的应用,综合性较强.利用函数奇偶性的定义和性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知∠A=60°,P、Q分别是∠A两边上的动点.
如图,已知∠A=60°,P、Q分别是∠A两边上的动点. PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米-75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区某年全年每天的PM2.5日均值检测数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据国家标准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米-75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区某年全年每天的PM2.5日均值检测数据中随机地抽取12天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)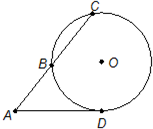 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4