题目内容
 如图,已知∠A=60°,P、Q分别是∠A两边上的动点.
如图,已知∠A=60°,P、Q分别是∠A两边上的动点.(1)当AP=1,AQ=3时,求PQ的长;
(2)AP,AQ长度之和为定值4,求S△APQ最大值.
考点:余弦定理的应用,基本不等式在最值问题中的应用
专题:三角函数的求值
分析:(1)∠A=60°,AP=1,AQ=3,由余弦定理即可求得PQ的长;(2))由AP+AQ≥2
,得AP•AQ≤4从而S△APQ=
AP•AQsinA≤
•4•
=
.
| AP•AQ |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解答:
解:(1)∵)∠A=60°,AP=1,AQ=3,
∴由余弦定理得:PQ2=PA2+AQ2-2AP•AQcos60°=1+9-2×1×3×
=7,
∴PQ=
;
(2)∵AP+AQ≥2
,∴AP•AQ≤4
∴S△APQ=
AP•AQsinA≤
•4•
=
.
∴由余弦定理得:PQ2=PA2+AQ2-2AP•AQcos60°=1+9-2×1×3×
| 1 |
| 2 |
∴PQ=
| 7 |
(2)∵AP+AQ≥2
| AP•AQ |
∴S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题考查余弦定理,关键在于熟练掌握余弦定理并灵活运用之,基本不等式的应用问题,本题是一道基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
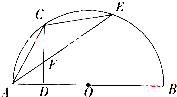 如图,半圆O的直径AB的长为4,点C平分弧AE,过C作AB的垂线交AB于D,交AE干F.
如图,半圆O的直径AB的长为4,点C平分弧AE,过C作AB的垂线交AB于D,交AE干F.